Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M(x; y) là điểm thuộc đường phân giác tạo bởi 2 đường thẳng đã cho.
![]()
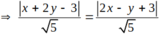
![]()
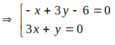
Chọn C.

1. Tìm cosin góc giữa 2 đg thẳng denta 1 : 10x +5y -1=0 và denta 2 : x = 2+t ; y = 1-t
\(\Delta\left(1\right):10x+5y-1=0\)
\(\Delta\left(2\right):\left\{{}\begin{matrix}x=2+t\\y=1-t\end{matrix}\right.\)
\(\Delta\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}t=x-2\\y=1-\left(x-2\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}t=x-2\\y=1-x+2\end{matrix}\right.\Leftrightarrow x+y-3=0\)
Ta có phương trình tổng quát của \(\Delta\left(2\right)\)là \(x+y-3=0\)
\(cos\left(\Delta\left(1\right),\Delta\left(2\right)\right)=\frac{\left|a_1.a_2+b_1.b_2\right|}{\sqrt{a_1^2+b_1^2}\sqrt{a_2^2+b_2^2}}\)
\(=\frac{\left|10+5\right|}{\sqrt{1+1}.\sqrt{100+25}}=\frac{15}{5\sqrt{10}}\)
Bấm SHIFT COS\(\left(\frac{15}{5\sqrt{10}}\right)\)=o'''
\(=18^o26'5,82''\)
bài 2,3,4 tương tự vậy.

Gọi d là phân giác góc hợp bởi d1 và d2
Điểm N bất kì thuộc d có tọa độ \(N\left(x;y\right)\Rightarrow d\left(N;d_1\right)=d\left(N;d_2\right)\)
\(\Rightarrow\frac{\left|3x+4y+1\right|}{\sqrt{3^2+4^2}}=\frac{\left|x-2y+4\right|}{\sqrt{1^2+\left(-2\right)^2}}\)
\(\Leftrightarrow\left|3x+4y+1\right|=\sqrt{5}\left|x-2y+4\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+4y+1=\sqrt{5}x-2\sqrt{5}y+4\sqrt{5}\\3x+4y+1=-\sqrt{5}x+2\sqrt{5}y-4\sqrt{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(3-\sqrt{5}\right)x+\left(4+2\sqrt{5}\right)y+1-4\sqrt{5}=0\\\left(3+\sqrt{5}\right)x+\left(4-2\sqrt{5}\right)y+1+4\sqrt{5}=0\end{matrix}\right.\)

1/ Gọi A là giao điểm của (d) và Ox \(\Rightarrow A\left(\frac{3}{2};0\right)\Rightarrow OA=\frac{3}{2}\)
Gọi B là giao điểm của (d) và Oy \(\Rightarrow B\left(0;-3\right)\Rightarrow OB=3\)
\(\Rightarrow S_{OAB}=\frac{1}{2}OA.OB=\frac{1}{2}.\frac{3}{2}.3=\frac{9}{4}\)
2/ Gọi C là giao điểm của (d) và Ox \(\Rightarrow C\left(1;0\right)\Rightarrow OC=1\)
Gọi D là giao điểm của (d) và Oy \(\Rightarrow D\left(0;-1\right)\Rightarrow OD=1\)
\(\Rightarrow S_{OCD}=\frac{1}{2}OC.OD=\frac{1}{2}\)

Gọi \(M\left(m;0\right)\) \(\Rightarrow d\left(M;d_1\right)=d\left(M;d_2\right)\)
\(\Rightarrow\frac{\left|3m-6\right|}{\sqrt{3^2+2^2}}=\frac{\left|3m+3\right|}{\sqrt{3^2+2^2}}\Rightarrow6-3m=3m+3\)
\(\Rightarrow m=\frac{1}{2}\Rightarrow M\left(\frac{1}{2};0\right)\)

- Xét phương trình hoành độ giao điểm : \(mx-4=-mx-4\)
\(\Leftrightarrow2mx=0\)
\(\Leftrightarrow x=0\)
\(\Rightarrow y=-4\)
=> Tọa độ điểm ( 0; - 4 )
- d1 cắt trục hoành tại điểm : \(\left(\dfrac{4}{m};0\right)\)
- d2 cắt trục hoành tại điểm : \(\left(-\dfrac{4}{m};0\right)\)
=> Tam giác đó là tam giác cân .
\(\Rightarrow S=\dfrac{1}{2}.\left|-4\right|.\left|\dfrac{8}{m}\right|=\left|\dfrac{16}{m}\right|>8\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{16}{m}< -8\\\dfrac{16}{m}>8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m\in\left(-2;0\right)\\m\in\left(0;2\right)\end{matrix}\right.\)
Vậy \(S=\left\{1\right\}\)
Lời giải:
PT đường phân giác đi qua điểm $O$ nên có dạng $y=kx$
Gọi $M$ là điểm nằm trên đường phân giác, có tọa độ $(a,b)$
Theo tính chất đường phân giác:
\(d(M,\Delta)=d(M,Ox)\)
\(\Leftrightarrow \frac{|a+b|}{\sqrt{1^2+1^2}}=\frac{|b|}{\sqrt{1^2+0^2}}\Leftrightarrow |a+b|=\sqrt{2}|b|\)
\(\Rightarrow \left[\begin{matrix} a+b=\sqrt{2}b\\ a+b=-\sqrt{2}b\end{matrix}\right.\Rightarrow \left[\begin{matrix} a=b(\sqrt{2}-1)\\ a=b(-\sqrt{2}-1)\end{matrix}\right.\Rightarrow \left[\begin{matrix} b=(1+\sqrt{2})a\\ b=(1-\sqrt{2})a\end{matrix}\right.\)
Do đó PT đường phân giác có dạng
$y=(1+\sqrt{2})x$ hoặc $y=(1-\sqrt{2})x$