Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Tìm tọa độ của w → có giá vuông góc với đường thẳng d để d 1 là ảnh của d qua T w →
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có: n P → = n α → ; n P → = 2 ; - 1 ; 2 ⇒ P : 2 x - y + 2 z + D = 0
Mặt cầu (S) có tâm I 1 ; - 3 ; 2 ; R = 4 ⇒ d I ; P = 4 ⇔ 9 + D 4 + 1 + 4 = 4 ⇔ [ D = 3 D = - 21

Trong 4 cách sau :
1. Giảm chiều cao kê mặt phẳng nghiêng
2. Tăng chiều cao kê mặt phẳng nghiêng
3. Giảm độ dài của mặt phẳng nghiêng
4. Tăng độ dài của mặt phẳng nghiêng
Các cách nào làm giảm độ nghiêng của mặt phẳng nghiêng ?
A. Các cách 1 và 3
B. Các cách 1 và 4
C. Các cách 2 và 3
D. Các cách 2 và 4
Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Đường thẳng d 2 qua M vuông góc với có vectơ chỉ phương là v → = ( 2 ; − 3 ) .
Do đó phương trình của d 2 là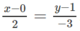 .
.
Gọi M' là giao của d 1 với d 2 thì tọa độ của nó phải thỏa mãn hệ phương trình:
Từ đó suy ra