Question

[Pham Trong Bach]

Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; − 3 và mặt phẳng P : 2 x + 2 y − z + 9 = 0 . Đường thẳng d đi qua A và có vectơ chỉ phương u → = 3 ; 4 − 4 cắt P tại điểm B. Điểm M thay đổi trong P sao cho M luôn nhìn đoạn AB dưới góc 90 0 .  Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau?

A.  J − 3 ; 2 ; 7

B.  K 3 ; 0 ; 15

C.  H − 2 ; − 1 ; 3

D.  I − 1 ; − 2 ; 3

Answer 1

[Cao Minh Tâm]

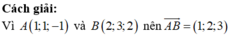
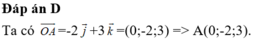
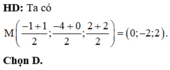
Đáp án D

Phương trình đường thẳng

d : x − 1 3 − = y − 2 4 = z + 3 − 4 .

 Vì 

B ∈ d ⇒ B 3 b + 1 ; 4 b + 2 ; − 4 b − 3

Mà B = d ∩ P suy ra

2 3 b + 1 + 2 4 b + 2 + 4 b + 3 + 9 = 0 ⇔ b = − 1 ⇒ B − 2 ; − 2 ; 1

Gọi A’là hình chiếu của A trên

P ⇒ A   A ' : x − 1 2 = y − 2 2 = z + 3 − 1 ⇒ A ' − 3 ; − 2 ; − 1  

Theo bài ra, ta có 

M A 2 + M B 2 = A B 2 ⇔ M B 2 = A B 2 − M A 2 ≤ A B 2 − A   A ' 2 = A ' B 2

Độ dài MB lớn nhất khi  

M ≡ A ' ⇒ M B : x = − 2 + t y = − 2 z = 1 + 2 t ⇒ I − 1 ; − 2 ; 3 ∈ M B