Hai vật dao động điều hòa cùng pha ban đầu, cùng phương và cùng thời điểm với các tần số góc lần lượt là ω1 = π/6 rad/s; ω2 = π/3 rad/s. Chọn gốc thời gian lúc hai vật đi qua vị trí cân bằng theo chiều dương. Thời gian ngắn nhất mà hai vật gặp nhau là:
A. 1s.
B. 4s.
C. 2s.
D. 8s.

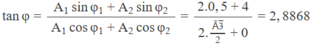
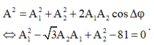
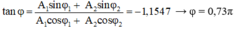


Chọn C
+ Phương trình dao động của hai vật:
x1 = A1 cos(ω1t - π/2)
x2 = A2 cos(ω2t - π/2)
+ Hai vật gặp nhau lần đầu khi pha của chúng đối nhau: ω1t - π/2 = - (ω2t - π/2)
=> (ω1 + ω2 ).t = π => t = 2s.