Cho góc A = 90o . Gọi B ; C là các điểm thuộc hai cạnh của góc A , điểm D nằm giữa B và C ; điểm E nằm giữa B và D biết \(\widehat{BAE}\) = 20o , \(\widehat{EAD}\) = 30o . Tính \(\widehat{DAC}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
7 tháng 1 2018
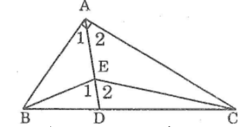
Kéo dài AE cắt BC tại D
Trong ∆ABE ta có ∠E1 là góc ngoài tại đỉnh E
Suy ra: ∠E1 > ∠A1 (tính chất góc ngoài tam giác)(1)
Trong ∆AEC ta có ∠E2 là góc ngoài tại đỉnh E
Suy ra: ∠E2 > ∠A2 (tính chất góc ngoài tam giác)(2)
Cộng từng vế (1) và (2) ta có:
∠E1 + ∠E2 > ∠A1 +∠A2
Hay ∠ (BEC) > ∠ (BAC) = 90º
Vậy góc (BEC) là góc tù.
AH
Akai Haruma
Giáo viên
6 tháng 2 2024
Lời giải:
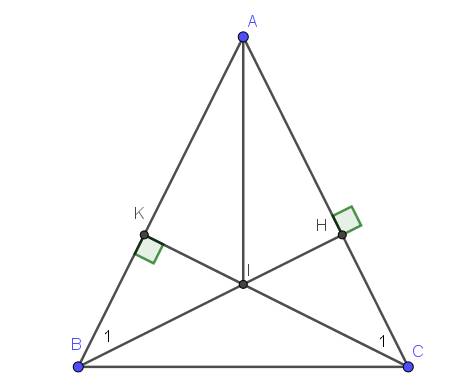
a. Xét tam giác $ABH$ và $ACK$ có:
$AB=AC$
$\widehat{A}$ chung
$\widehat{AHB}=\widehat{AKC}=90^0$
$\Rightarrow \triangle ABH=\triangle ACK$ (ch-gn)
$\Rightarrow AH=AK$
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{B_1}=\widehat{C_1}$
Vì $AB=AC; AK=AH\Rightarrow AB-AK=AC-AH$
$\Rightarrow BK=CH$
Xét tam giác $KBI$ và $HCI$ có:
$\widehat{B_1}=\widehat{C_1}$
$\widehat{BKI}=\widehat{CHI}=90^0$
$BK=CH$
$\Rightarrow \triangle KBI=\triangle HCI$ (c.g.c)
$\Rightarrow BI=CI$
Xét tam giác $ABI$ và $ACI$ có:
$AB=AC$
$AI$ chung
$BI=CI$
$\Rightarrow \triangle ABI=\triangle ACI$ (c.c.c)
$\Rightarrow \widehat{BAI}=\widehat{CAI}$
$\Rightarrow AI$ là phân giác $\widehat{A}$
$
Lời giải:
$\widehat{DAC}=\widehat{BAC}-\widehat{BAE}-\widehat{EAD}=90^0-20^0-30^0=40^0$