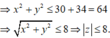Gọi z 1 ; z 2 là các nghiệm phức của phương trình z 2 + 4 z + 7 = 0 . Số phức z 1 z 2 + z 1 z 2 bằng
A. 2
B. 10
C. 2i
D. 10i
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


![]()

Đáp án A.
Do ![]() nên tập hợp điểm M là các điểm nằm ngoài đường tròn
nên tập hợp điểm M là các điểm nằm ngoài đường tròn ![]() và nằm trong đường tròn
và nằm trong đường tròn 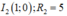
Dựa vào hình vẽ ta chứng minh được ![]()
Khi đó ![]()

Đáp án A.
Ta có ![]()
![]()
![]()
Lấy môđun hai vế, ta được ![]()
![]()
Đặt ![]() khi đó (*)
khi đó (*) ![]()
![]()
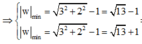
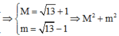
![]()

Đáp án A.
Ta có 1 = z - 2 - 3 i 2 = z - 2 - 3 i . z - 2 - 3 i ¯ = z - 2 - 3 i z ¯ - 2 + 3 i ¯ = z - 2 - 3 i z ¯ - 2 + 3 i
Lấy môđun hai vế, ta được z - 2 - 3 i . z ¯ - 2 + 3 i = 1 ⇔ z ¯ - 2 + 3 i = 1 ( * )
Đặt w = z ¯ + 1 + i ⇔ z ¯ = w - 1 - i , khi đó (*) ⇔ w - 1 - 2 - 3 i = 1 ⇔ w - 3 + 2 i = 1 .
⇒ w m i n = 3 2 + 2 2 - 1 = 13 - 1 w m i n = 3 2 + 2 2 - 1 = 13 + 1 ⇒ M = 13 + 1 m = 13 - 1 ⇒ M 2 + m 2 = 13 + 1 2 + 13 - 1 2 = 28 .

\(z^2-4z+5=0\Rightarrow\left\{{}\begin{matrix}z_1+z_2=4\\z_1z_2=5\end{matrix}\right.\) theo hệ thức Viet
\(w=\dfrac{z_1+z_2}{z_1z_2}+i.z_1z_2\left(z_1+z_2\right)=\dfrac{4}{5}+i.5.4=\dfrac{4}{5}+20i\)

Đáp án D
Cách giải: gọi z=x+yi
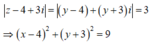
Vậy quỹ tích các điểm z thuộc đường tròn tâm I(4;-3); R=3
Đặt 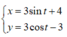
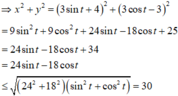
(theo bunhiacopxki)