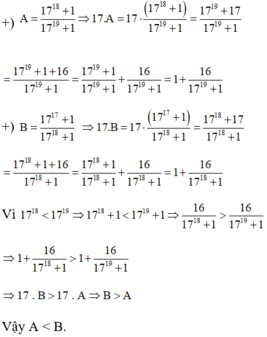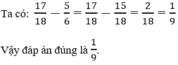so sánh :A=1718+1/1719+1; B=1717+1/1718+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
NM
2
19 tháng 6 2018
a) Ta có :
\(\frac{1717\div101}{1919\div101}=\frac{17}{19}\)
Vậy : \(\frac{17}{19}=\frac{1717}{1919}\)
b) Ta có :
4222 = ( 22)222 = 2444
Do 2444 = 2444
Suy ra 2444 = 4222
Vậy : 2444 = 4222
26 tháng 2 2015
Ta có \(\frac{-17}{-19}=\frac{\left(-17\right).\left(-101\right)}{\left(-19\right).\left(-101\right)}=\frac{1717}{1919}\)
mà \(\frac{1717}{1919}
AH
Akai Haruma
Giáo viên
6 tháng 1
Lời giải:
\(\frac{1719}{3976}=\frac{1}{2+\frac{538}{1719}}=\frac{1}{2+\frac{1}{3+\frac{105}{538}}}=\frac{1}{2+\frac{1}{3+\frac{1}{5+\frac{13}{105}}}}=\frac{1}{2+\frac{1}{3+\frac{1}{5+\frac{1}{8+\frac{1}{13}}}}}\)
$\Rightarrow a=8; b=13$
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1
\(\dfrac{1719}{3976}=\dfrac{1}{\dfrac{3976}{1719}}=\dfrac{1}{2+\dfrac{538}{1719}}=\dfrac{1}{2+\dfrac{1}{\dfrac{1719}{538}}}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{105}{538}}}\)
\(=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{\dfrac{538}{105}}}}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5+\dfrac{13}{105}}}}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5+\dfrac{1}{\dfrac{105}{13}}}}}\)
\(=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5+\dfrac{1}{8+\dfrac{1}{13}}}}}\)
HN
Tính A=17/18+1718/1718+171717/181818+...+1717...17/1818...18(2018 chữ số 17 và 18). Ai làm đc tk cho
4
XO
11 tháng 8 2020
\(A=\frac{17}{18}+\frac{1717}{1818}+\frac{171717}{181818}+...+\frac{1717..17}{1818...18}\)(2018 số 17 và 18)
\(=\frac{17}{18}+\frac{17.101}{18.101}+\frac{17.10101}{18.10101}+...+\frac{17.1010...01}{18.1010...01}\)(2017 cặp số 10 liên tiếp và dư 1 số 1)
\(=\frac{17}{18}+\frac{17}{18}+\frac{17}{18}+...+\frac{17}{18}\left(2018\text{ số hạng}\right)\)
\(=\frac{17}{18}.2018=\frac{17153}{9}\)
CM
28 tháng 10 2017
Hướng dẫn giải:
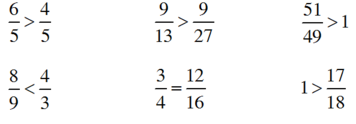
Giải thích:
+ 
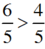vì cùng có mẫu bằng 5, tử số 6 > 4.
+ 
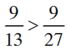vì có cùng tử số, mẫu số 13 < 27.
+ 
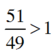vì tử số 51 > mẫu số = 49.
+ 
+ 
+ 
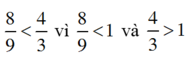
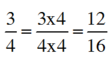
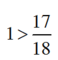vì tử số bằng 17 < mẫu số bằng 18.
T
2
31 tháng 7 2023
\(A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}\)
\(\dfrac{1}{2.2}< \dfrac{1}{1.2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3.3}< \dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)
\(\dfrac{1}{4.4}< \dfrac{1}{3.4}=\dfrac{1}{3}-\dfrac{1}{4}\)
...
\(\dfrac{1}{2009.2009}< \dfrac{1}{2008.2009}=\dfrac{1}{2008}-\dfrac{1}{2009}\)
\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...\dfrac{1}{2008}-\dfrac{1}{2009}=1-\dfrac{1}{2009}< 1\)
\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}< 1\)
31 tháng 7 2023
Ta có:
\(\dfrac{1}{2\times2}+\dfrac{1}{3\times3}+\dfrac{1}{4\times4}+...+\dfrac{1}{2009\times2009}< \dfrac{1}{1\times2}+\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+...+\dfrac{1}{2008\times2009}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2008}-\dfrac{1}{2009}=1-\dfrac{1}{2009}< 1\)
TT
0