Cho hàm số \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^3-4x^2+3}{x-1};\left(x\ne1\right)\\ax+\dfrac{5}{2};\left(x=1\right)\end{matrix}\right.\). Xác định \(a\) để hàm số liên tục trên \(R\)?
| A. \(a=\dfrac{5}{2}\). | B. \(a=-\dfrac{15}{2}\). | C. \(a=-\dfrac{5}{2}\). | D. \(a=\dfrac{15}{2}\). |



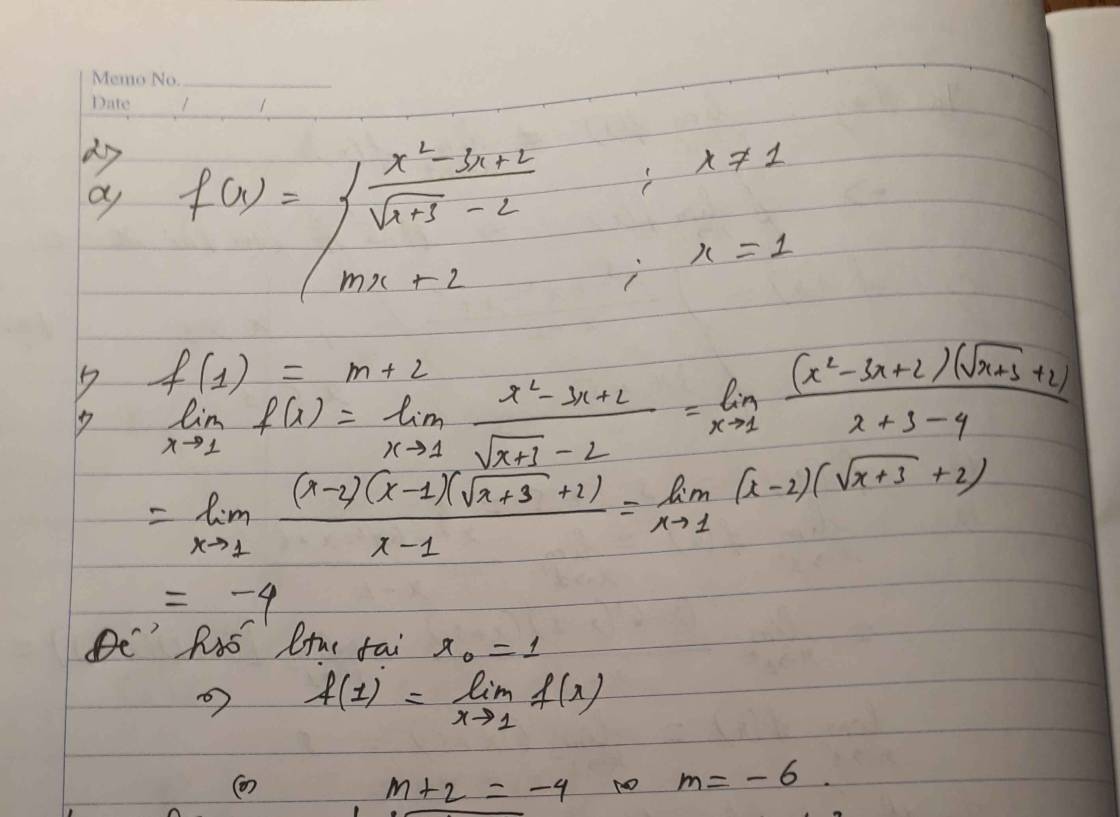
Lời giải:
Khi \(x\neq 1\) thì hàm \(f(x)\) luôn là hàm sơ cấp xác định nên $f(x)$ liên tục tại mọi điểm \(x\neq 1\).
Do đó để hàm liên tục trên \(\mathbb{R}\Rightarrow \) chỉ cần xác định $a$ để hàm liên tục tại điểm $x=1$ là đủ.
Để $f(x)$ liên tục tại $x=1$ thì:
\(\lim_{x\to 1}f(x)=f(1)\)
\(\Leftrightarrow \lim_{x\to 1}\frac{x^3-4x^2+3}{x-1}=a+\frac{5}{2}\)
\(\Leftrightarrow \lim_{x\to 1}\frac{(x-1)(x^2-3x-3)}{x-1}=a+\frac{5}{2}\)
\(\Leftrightarrow \lim_{x\to 1}(x^2-3x-3)=a+\frac{5}{2}\)
\(\Leftrightarrow -5=a+\frac{5}{2}\Leftrightarrow a=\frac{-15}{2}\)
Đáp án B