Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ:
A B C D
Xét tam giác ABC và tam giác ACD có:
AC: cạnh chung
góc BAC = góc ACD (AB // CD)
góc DAC = góc ACB (AD // BC)
=> tam giác ABC = tam giác ADC
=> AB = DC = 2,5 cm
ta có: tam giác ABC = tam giác ADC
=> BC = AD = 3,5 cm
Chu vi tam giác ACD:
AC + AD + CD = 2,5 cm + 3,5 cm + 3 cm
= 9 cm
Vậy chu vi tam giác ACD là 9 cm.

Vẽ tượng trưng thôi nhé, mk không chắc là đúng số đo đâu
Ta có hình vẽ:
A B C x t D
Chu vi tam giác ABC:
AB + AC + BC = 2,5 + 3 + 3,5 = 9 (cm)
Ta có: x//BC
nên \(\widehat{CAD}\)=\(\widehat{ACB}\) (so le trong)
Ta có: t//AB
nên \(\widehat{BAC}\)=\(\widehat{ACD}\) (so le trong)
Xét tam giác ABC và tam giác ACD có:
AC: cạnh chung
\(\widehat{CAD}\)=\(\widehat{ACB}\) (đã chứng minh)
\(\widehat{BAC}\)=\(\widehat{ACD}\) (đã chứng minh)
=> tam giác ABC = tam giác ACD (g.c.g)
Vì tam giác ABC = tam giác ACD
mà chu vi tam giác ABC = 9 cm
nên chu vi tam giác ACD = 9 cm

1)

a) Ta có: góc BAD+góc CAE+góc BAC=180 độ
Mà góc BAC=90 độ nên góc BAD+ góc CAE=90 độ (1)
Vì tam giác ACE vuông tại E nên góc ACE+góc CAE=90 độ(2)
Từ (1) và (2) => góc BAD= góc ACE
Xét tam giác ABD và tam giác ACE có:
góc ADB=góc AED=90 độ
AB=AC ( vì tam giác ABC vuông cân tại A)
góc BAD=góc ACE (cmt)
=> tam giác ABD=tam giác ACE (cạnh huyền-góc nhọn)
b) Theo câu a) Tam giác ABD=tam giác ACE
=> DA=EC và BD=AE
Mà DE=DA+AE nên DE=EC+BD

bạn tự vẽ hình nha
a) Áp dụng định lý Pi-ta-go cho tam giác ABC vuông tại A
=> \(AB^2+AC^2=BC^2\)
\(3^2+4^2=BC^2\)
\(9+16=BC^2\)
=> \(BC^2=25\)
=>\(BC=5\)
b) Xét tam giác ABD và tam giác EBD có:
\(\widehat{BAD}=\widehat{BED}\left(=90độ\right)\)
BD chung
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
=> tam giác ABD = tam giác EBD (ch-gn)
c)Vì tam giác ABD = tam giác EBD
=>\(BA=BE\left(1\right)\)
Theo đề bài ta có:
\(AK=EC\left(2\right)\)
Cộng 2 vế của (1),(2)
=>\(BA+AK=BE+EC\)
\(BK=BE\)
=> tam giác BKC cân
=>\(\widehat{BKC}=\widehat{BCK}\)
d)Xét tam giác BAI và tam giác BEI có:
IB chung
\(\widehat{ABI}=\widehat{EBI}\left(gt\right)\)
\(AB=BE\)
=> tam giác BAI = tam giác BEI (c-g-c)
=>AI = EI


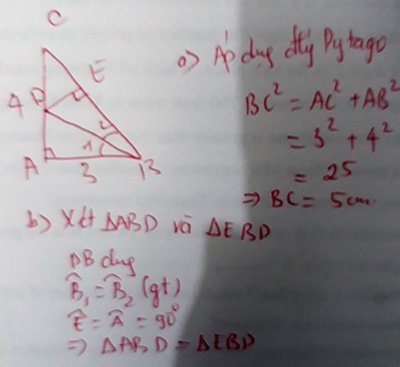
ko nhá