Question

[Nguyễn Minh Phong]

Cho hình thang ABCD có độ dài đáy AB=5cm; CD=3cm. Các điểm M, N lần lượt nằm trên các cạnh AD và BC sao cho MA= 1/4 AD, NB= 1/4BC. Nối M với N, ta được hai hình thang ABNM và CDMN. S của ABCD =16cm2. Tính độ dài MN.

Answer 1

[Nguyễn Ngọc Anh Minh]

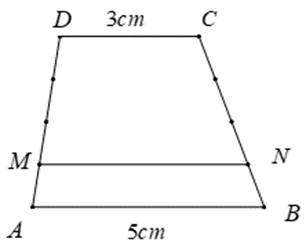
Hai tg ACD và tg ABC có đường cao từ A->CD = đường cao từ C->AB nên

\(\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{CD}{AB}=\dfrac{3}{5}\)

\(S_{ABCD}=S_{ACD}+S_{BCD}\)

\(\Rightarrow S_{ACD}=\dfrac{3}{3+5}xS_{ABCD}=\dfrac{3}{8}xS_{ABCD}=\dfrac{3}{8}x16=6cm^2\)

\(\Rightarrow S_{ABC}=S_{ABCD}-S_{ACD}=16-6=10cm^2\)

Hai tg ACD và tg BCD có đường cao từ A->CD = đường cao từ B->CD và chung cạnh CD

\(\Rightarrow S_{ACD}=S_{BCD}=6cm^2\)

C/m tương tự ta cũng có 

\(S_{ABC}=S_{ABD}=10cm^2\)

Hai tg ABN và tg ABC có chung đường cao từ A->BC nên

\(\dfrac{S_{ABN}}{S_{ABC}}=\dfrac{BN}{BC}=\dfrac{1}{4}\Rightarrow S_{ABN}=\dfrac{1}{4}xS_{ABC}=\dfrac{1}{4}x10=2,5cm^2\)

đường cao từ N->AB là

\(\dfrac{2xS_{ABN}}{AB}=\dfrac{2x2,5}{5}=1cm\)

Hai tg NCD và tg BCD có chung đường cao từ D->BC nên

\(\dfrac{S_{NCD}}{S_{BCD}}=\dfrac{CN}{BC}=\dfrac{3}{4}\Rightarrow S_{NCD}=\dfrac{3}{4}xS_{BCD}=\dfrac{3}{4}x6=4,5cm^2\)

\(S_{ADN}=S_{ABCD}-S_{ABN}-S_{CDN}=16-2,5-4,5=9cm^2\)

Hai tg AMN và tg ADN có chung đường cao từ N->AD nên

\(\dfrac{S_{AMN}}{S_{ADN}}=\dfrac{AM}{AD}=\dfrac{1}{4}\Rightarrow S_{AMN}=\dfrac{1}{4}xS_{ADN}=\dfrac{1}{4}x9=2.25cm^2\)

\(S_{ABNM}=S_{ABN}+S_{AMN}=2,5+2,25=4,75cm^2\)

Như vậy ta biết diện tích hình thang ABNM, biết đáy lớn AB, biết đường cao (đường cao từ N->AB). Áp dụng công thức tính diện tích hình thang sẽ tính được đáy nhỏ MN. 

Bạn tự tính nốt nhé

Answer 2

[Thắng]

Sabcd = 16cm² => (3+5)xHabcd =32 cm => Habcd = 4cm.

Điểm M và N lần lượt = 1/4 AD và BC nên chiều cao ABNM = 4:4 = 1cm. Chiều cao CD đến MN = 4-1= 3cm

Ta có: Sabnm + Smncd = 16cm² => (5+mn)+ (3+mn)x3 = 32cm

4mn+14=32cm => mn=4,5cm