Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.

Mình nghĩ khó mà có người giải hết chỗ bài tập đấy của bạn, nhiều quá
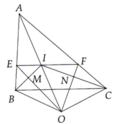
3/ (Bạn tự vẽ hình giùm)
a/ \(\Delta ABC\)và \(\Delta ADC\)có:
\(\widehat{BAC}=\widehat{ACD}\)(AB // DC; ở vị trí so le trong)
Cạnh AC chung
\(\widehat{CAD}=\widehat{ACB}\)(AB // DC; ở vị trí so le trong)
=> \(\Delta ABC\)= \(\Delta ADC\)(g. c. g)
=> AD = BC (hai cạnh tương ứng)
và AB = DC (hai cạnh tương ứng)
b/ Ta có AD = BC (cm câu a)
và \(AN=\frac{1}{2}AD\)(N là trung điểm AD)
và \(MC=\frac{1}{2}BC\)(M là trung điểm BC)
=> AN = MC
Chứng minh tương tự, ta cũng có: BM = ND
\(\Delta AMB\)và \(\Delta CND\)có:
BM = ND (cmt)
\(\widehat{ABM}=\widehat{NDC}\)(AB // CD; ở vị trí so le trong)
AB = CD (\(\Delta ABC\)= \(\Delta ADC\))
=> \(\Delta AMB\)= \(\Delta CND\)(c. g. c)
=> \(\widehat{BAM}=\widehat{NCD}\)(hai góc tương ứng)
và \(\widehat{BAC}=\widehat{ACN}\)(\(\Delta ABC\)= \(\Delta ADC\))
=> \(\widehat{BAC}-\widehat{BAM}=\widehat{ACN}-\widehat{NCD}\)
=> \(\widehat{MAC}=\widehat{ACN}\)(1)
Chứng minh tương tự, ta cũng có \(\widehat{AMC}=\widehat{ANC}\)(2)
và AN = MC (cmt) (3)
=> \(\Delta MAC=\Delta NAC\)(g, c. g)
=> AM = CN (hai cạnh tương ứng) (đpcm)
c/ \(\Delta AOB\)và \(\Delta COD\)có:
\(\widehat{BAO}=\widehat{OCD}\)(AB // DC; ở vị trí so le trong)
AB = CD (cm câu a)
\(\widehat{ABO}=\widehat{ODC}\)(AD // BC; ở vị trí so le trong)
=> \(\Delta AOB\)= \(\Delta COD\)(g. c. g)
=> OA = OC (hai cạnh tương ứng)
và OB = OD (hai cạnh tương ứng)
d/ \(\Delta ONA\)và \(\Delta MOC\)có:
\(\widehat{AON}=\widehat{MOC}\)(đối đỉnh)
OA = OC (O là trung điểm AC)
\(\widehat{OAN}=\widehat{OCM}\)(AM // NC; ở vị trí so le trong)
=> \(\Delta ONA\)= \(\Delta MOC\)(g. c. g)
=> ON = OM (hai cạnh tương ứng)
=> O là trung điểm MN
=> M, O, N thẳng hàng (đpcm)

cau 1 :
Xet tam giac ABD va tam giac EBD co : BD chung
goc ABD = goc DBE do BD la phan giac cua goc ABC (gt)
AB = BE (Gt)
=> tam giac ABD = tam giac EBD (c - g - c)
=> goc BAC = goc DEB (dn)
ma goc BAC = 90 do tam giac ABC vuong tai A (gt)
=> goc DEB = 90
=> DE _|_ BC (dn)
b, tam giac ABD = tam giac EBD (cau a)
=> AB = DE (dn)
AB = 6 (cm) => DE = 6 cm
DE _|_ BC => tam giac DEC vuong tai E
=> DC2 = DE2 + CE2 ; DC = 10 cm (gt); DE = 6 cm (cmt)
=> CE2 = 102 - 62
=> CE2 = 64
=> CE = 8 do CE > 0

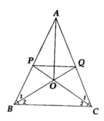

a, BQ là đường phân giác của góc B
=> \(\widehat{B_1}=\widehat{B_2}=\dfrac{1}{2}\widehat{B}\) ( 1 )
CP là đường phân giác của góc C
=> \(\widehat{C_1}=\widehat{C_2}=\dfrac{1}{2}\widehat{C}\) ( 2 )
Mà tam giác ABC cân tại A
= > \(\widehat{B}=\widehat{C}\) ( 3 )
Từ ( 1 ) , ( 2 ) , ( 3 ) = > \(\widehat{B_1}=\widehat{B_2}=\widehat{C_1}=\widehat{C_2}\)
Xét tam giác OBC có :
\(\widehat{B_2}=\widehat{C_2}\) ( cmt )
= > Tam giác OBC cân tại O
b, Do O là giao của 2 đường phân giác BQ và CP của tam giác ABC
nên O là trực tâm của tam giác ABC hay điểm O cách đều 3 cạnh AB,AC, BC của tam giác ABC
c, Do O là trực tâm của tam giác ABC ( câu b, )
Mà tam giác ABC cân tại A
= > AO vừa là đường cao vừa là đường trung tuyến của tam giác ABC tức là AO đi qua trung điểm của đoạn thẳng BC
d, Xét \(\Delta QBC\) và \(\Delta PCB\) có :
\(\widehat{B_2}=\widehat{C_2}\left(cmt\right)\)
BC chung
\(\widehat{B}=\widehat{C}\left(gt\right)\)
=> \(\Delta QBC=\Delta PCB\left(g-c-g\right)\)
= > CP = BQ ( 2 cạnh tương ứng )
e, Do tam giác QBC = tam giác PCB ( câu d, )
=> BP = CQ ( 2 cạnh tương ứng )
\(P\in AB\)
= > AP + PB = AB
= > AP = AB - PB ( 4 )
\(Q\in AC\)
= > AQ + QC =AC
= > AQ = AC - QC ( 5 )
Từ ( 4 ) , ( 5 )
= > AP = AQ
Xét tam giác APQ có :
AP = AQ ( cmt )
= > Tam giác APQ cân tại A ( đpcm )
a) △���△ABC cân tại �A nên ���^=���^ABC=ACB.
Vì ��BQ và ��CP là đường phân giác của �^,�^B,C nên �1^=�2^=���^2B1=B2=2ABC, �1^=�2^=���^2C1=C2=2ACB.
Do đó �1^=�2^=�1^=�2^B1=B2=C1=C2.
Suy ra △���△OBC cân tại �O.
b) Vì �O là giao điểm các đường phân giác ��CP và ��BQ trong △���△ABC nên �O là giao điểm ba đường phân giác trong △���△ABC.
Do đó, �O cách đều ba cạnh ��,��AB,AC và ��BC.
c) Ta có △���△ABC cân tại �,��A,AO là đường phân giác của góc �A nên ��AO đồng thời là trung tuyến và đường cao của △���△ABC.
Vậy đường thẳng ��AO đi qua trung điểm của đoạn thẳng ��BC và vuông góc với nó.
d) Ta có △���=△���△PBC=△QCB (g.c.g)
⇒��=��⇒CP=BQ (hai cạnh tương ứng).
e) Ta có ��=��−��AP=AB−BP, ��=��−��AQ=AC−CQ (1);
△���=△���⇒��=��△PBC=△QCB⇒BP=CQ (2).
Lại có ��=��AB=AC (tam giác ���ABC cân tại �A) (3).
Từ (1), (2) và (3) suy ra ��=��AP=AQ.
Vậy tam giác ���APQ cân tại �A.