Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : HCK = HBC (cùng phụ với ^BKC) (1)
HCB+HBC=90* (hai góc nhọn trong tam giác vuông)
BCA+CBA=90* (hai góc nhọn trong tam giác vuông)
Nên HCB+HBC+BCA+CBA=90+90*=180*
Hay HCA+HBA=180*
Mà HBx + HBA=180* (hai góc kề bù)
Do đó HCA=^HBx (2)
Mà HBC=^HBx (do By là phân giác) (3)
Vay từ (1), (2), (3) suy ra HCK = HCA (đpcm)

Xét ΔABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(Định lí tổng ba góc của một tam giác)
=>\(100^o+40^o+\widehat{A}=180^O\)
\(\Rightarrow\widehat{A}=40^o\)
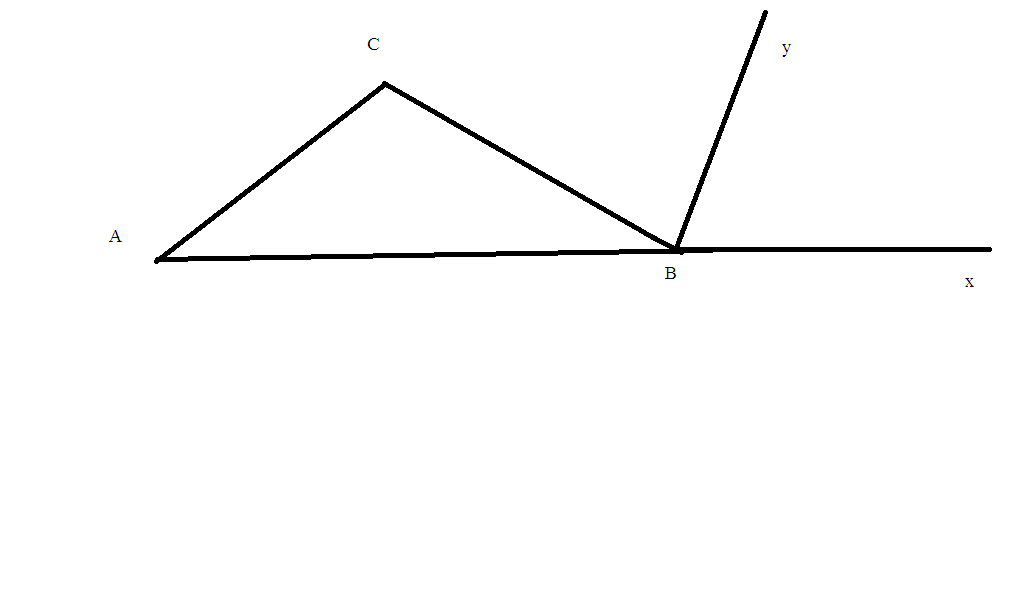
a)Xét ΔABC có \(\widehat{xBC}\) là góc ngoài tam giác ABC tại đỉnh B, ta có:
\(\widehat{xBC}=\widehat{C}+\widehat{A}\)
\(\Rightarrow\widehat{xBC}=40^o+100^o=140^o\)
b)Chứng minh // thì đc chứ ⊥ thì, xem lại đề nhé bn

Ta có : HCK = HBC ( cùng phụ với BKC) (1)
HCB + HBC = 90° ( tổng các góc trong ∆)
BCA + CBA = 90° ( tổng các góc trong ∆)
=> HCB + HBC + BCA + CBA = 180°
Hay HCA + HBA = 180°
Mà HBx + HBA = 180° ( kề bù)
Do đó : HCA = HBx (2)
Mà HBC = HBx ( By là phân giác) (3)
Từ (1)(2)(3) => HCK = HCA
Ta có : HCK = HBC ( cùng phụ với BKC) (1)
HCB + HBC = 90° ( tổng các góc trong ∆)
BCA + CBA = 90° ( tổng các góc trong ∆)
=> HCB + HBC + BCA + CBA = 180°
Hay HCA + HBA = 180°
Mà HBx + HBA = 180° ( kề bù)
Do đó : HCA = HBx (2)
Mà HBC = HBx ( By là phân giác) (3)
Từ (1)(2)(3) => HCK = HCA
Góc xBC là góc ngoài của tam giác ABC tại đỉnh B
=> góc xBC + CBA = 180o
=> xBC = 180o - CBA = 180o - 80o = 100o
Mà By là tia p/g của góc xBC nên góc xBy = 1/2. xBC = 1/2 . 100o = 50o = góc BAC
Mà 2 góc này ở vị trí đồng vị nên By // AC