


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài làm :
a) Ta có :
\(\widehat{ACB}\text{ là góc nội tếp chắn nửa đường tròn}\)
\(\Rightarrow\widehat{ACB}=90^o\Rightarrow\widehat{ACM}=180^o-\widehat{ACB}=90^o\)
Từ đó ; ta có :
\(\widehat{ACM}+\widehat{AHM}=90+90=180^o\)
=> Tứ giác AHMC là tứ giác nội tiếp đường tròn vì có 2 góc đối diện = 180 độ
=> Điều phải chứng minh
b) Theo phần a : Tứ giác AHMC là tứ giác nội tiếp
\(\Rightarrow\widehat{AMH}=\widehat{ACH}\left(1\right)\)
Xét đường tròn (O) : Góc ADC và góc ABC đều là 2 góc nội tiếp cùng chắn cung AC
\(\Rightarrow\widehat{ADC}=\widehat{ABC}\left(2\right)\)
Vì CD⊥AB ; MH⊥AB
=> CD//MH
=>∠ADC = ∠AMH ( 2góc so le trong ) (3)
Từ (1) ; (2) ; (3)
\(\Rightarrow\widehat{ABC}=\widehat{ACH}\)
=> Điều phải chứng minh
c)∠AOC = 45o
=>∠COB = 180 - 45 = 135o
\(\Rightarrow S_{OCB}=\frac{\pi.R^2.n}{360}=\frac{\pi.2^2.135}{360}=\frac{3}{2}\pi\left(cm^2\right)\)
a) Xét tứ giác AHMC có
góc ACM + góc AHM = 180 độ
Vậy tứ giác AHMC nội tiếp

a. Xét (O) , có:
CD \(\perp\)AB = {H}
=> \(\widehat{CHA}=90^o\Rightarrow\widehat{CHE}=90^o\)
Có: \(\widehat{CMD}\)là góc nội tiếp chắn nửa đường tròn đường kính CD
=> \(\widehat{CMD}=90^o\Rightarrow\widehat{CME}=90^o\)
Xét tứ giác CMEH, có:
\(\widehat{CME}+\widehat{CHE}=90^o+90^o=180^o\)
2 góc \(\widehat{CME}\)và \(\widehat{CHE}\)là 2 góc đối nhau
=> CMEH là tứ giác nội tiếp (đpcm)
Câu a: Có góc CHE=90 độ (vì CD\(\perp AB\) tại H)
Góc CMD =90 độ(góc nt chắn nửa đt)
Mà góc CHE và góc CMD ở vị trí đối nhau
⇒ Tứ giác CMEH nội tiếp
Câu b:
Xét \(\Delta NACva\Delta NMB\) có :
Góc N chung
Góc NCA = góc NBM (cùng chắn cung MA)
⇒ \(\Delta NAC\) đồng dạng \(\Delta NBM\) (góc góc)
⇒\(\dfrac{NM}{NA}\)=\(\dfrac{NB}{NC}\)⇔NM.NC=NA.NB
Câu c:
Có góc PMA=90 độ ( góc nt chắn nửa đt)→PM\(\perp\)AK
Mà IK\(\perp\)AK
⇒IK song song với MP (từ vuông góc đến song song

a:
Gọi O là trung điểm của AB
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>BD vuông góc AC tại D
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE vuông góc BC tại E
Xét tứ giác CDHE có
góc CDH+góc CEH=180 độ
=>CDHE nội tiếp
b: Xét ΔCAB có
AE,BD là đường cao
AE cắt BD tại H
=>H là trực tâm
=>CH vuông góc AB tại K
c: Xét ΔAKH vuông tại K và ΔAEB vuông tại E có
góc KAH chung
Do đó: ΔAKH đồng dạng với ΔAEB
=>AK/AE=AH/AB
=>AH*AE=AK*AB
Xét ΔBKH vuông tại K và ΔBDA vuông tại D có
góc KBH chung
Do đó: ΔBKH đồng dạng với ΔBDA
=>BK/BD=BH/BA
=>BK*BA=BH*BD
AH*AE+BH*BD
=AK*AB+BK*BA
=BA^2
a) ....................... =) C, D, H, E cùng thuộc 1 đường tròn.
b) ....................... =) CH ⊥ AB.
c) ....................... =) AH.AE + BH.BD = AB2.

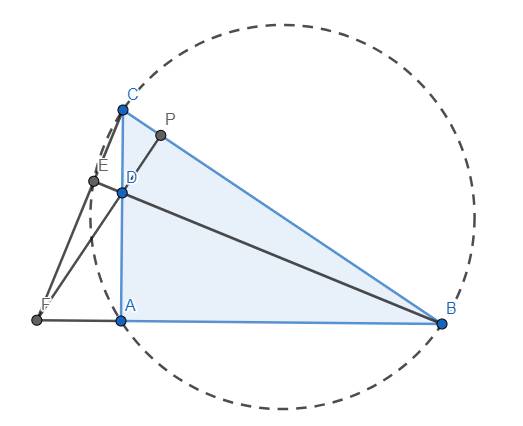
a) Ta có \(\widehat{CEB}=\widehat{CAB}=90^o\) nên 4 điểm A, B, C, E cùng thuộc đường tròn đường kính BC.
b) Kẻ \(FP\perp BC\) tại P. Ta thấy D là trực tâm tam giác FBC nên \(P\in DF\). Dễ thấy \(\Delta CDP~\Delta CBA\left(g.g\right)\) \(\Rightarrow\dfrac{CD}{CB}=\dfrac{CP}{CA}\) \(\Rightarrow CD.CA=CB.CP\)
CMTT, ta có \(BD.BE=BC.BP\)
Do đó \(CD.CA+BD.BE=CB.CP+BC.BP\) \(=BC\left(CP+BP\right)\) \(=BC^2\). Vậy đẳng thức được chứng minh.

a, Chứng minh: A B E ^ = A D E ^
b, Chứng minh được:
A
C
B
^
=
B
N
M
^
=> C, D, E nhìn AB dưới góc bằng nhau nên A, B, C, D, E cùng thuộc một đường tròn
=> BC là đường kính => B E C ^ = 90 0