K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 3 2019
\(3x^3+xy=3\)
\(\Leftrightarrow x\left(3x^2+y\right)=3\)
Với x = 1
\(\Rightarrow3x^2+y=3\Leftrightarrow y=0\)
Với x = 3
\(\Rightarrow3.3^2+y=3\)
\(\Leftrightarrow y=3-27=-24\)
Với x = -1
=> 3.(-1)^2+y=3
=>y=0
Với x = -3
=> y = -24
10 tháng 4 2019
Bài 1 dễ thì tự làm
Bài 2
\(y^2+2xy-3x-2=0\Leftrightarrow y^2+2xy+x^2=x^2+3x+2\)
\(\Leftrightarrow\left(x+y\right)^2=\left(x+1\right)\left(x+2\right)\)
Vế trái là số chính phương vế phải là tích 2 số nguyên liên tiếp nên 1 trong 2 số x+1 và x+2 phải có 1 số bàng 0
\(\Rightarrow y=-x\)
\(\orbr{\begin{cases}x+1=0\\x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=-2\end{cases}\Rightarrow\orbr{\begin{cases}y=1\\y=2\end{cases}}}}\)
Vậy \(\left(x;y\right)=\left(-1;1\right);\left(-2;2\right)\)
PD
1
25 tháng 9 2018
\(E=x^2+2xy+y^2-6x-6y+2017\)
\(=\left(x^2+2xy+y^2\right)-\left(6x+6y\right)+2017\)
\(=\left(x+y\right)^2-6\left(x+y\right)+2017\)
\(=\left(x+y\right)\left(x+y-6\right)+2017\)
3 tháng 9 2019
\(B=\left(x^2-8x\right)\left(x^2-8x+24\right)\)
Đặt \(x^2-8x+12=t\) ta có:
\(B=\left(t-12\right)\left(t+12\right)=t^2-144\ge-144\)
Dấu "=" xảy ra khi \(t^2=0\Leftrightarrow t=0\Leftrightarrow x^2-8x+12=0\)
\(\Leftrightarrow x^2-2x-6x+12=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-6\right)=0\Leftrightarrow x=2;x=6\)
3 tháng 9 2019
\(C=5x^2+9y^2-6xy-12x+13\)
\(=\left(x^2-6xy+9y^2\right)+\left(4x^2-12x+9\right)+4\)
\(=\left(x-3y\right)^2+\left(2x-3\right)^2+4\ge4\)
Dấu "=" xảy ra tại \(x=\frac{3}{2};y=\frac{1}{2}\)
19 tháng 8 2021
a) \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=\left(3x^2-6x+3\right)-\left(x^2+2x+1\right)+2\left(x^2-9\right)-\left(4x^2+12x+9\right)-5+20x\)
\(=-30\)
b) \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x\left(x^2+4x+4\right)+\left(4x^2+4x+1\right)+\left(x^3-3x^2+9x+3x^2-9x+27\right)-1\)
\(=27\)
19 tháng 8 2021
a: Ta có: \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=3x^2-6x+3-x^2-2x-1+2x^2-18-4x^2-12x-9-5+20x\)
\(=-30\)
b: Ta có: \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x^3-4x^2-4x+4x^2+4x+1+x^3+27-1\)
=27
H9
HT.Phong (9A5)
CTVHS
21 tháng 9 2023
c) \(\left(x+\dfrac{y}{x}\right)^3\)
\(=\left(\dfrac{x^2}{x}+\dfrac{y}{x}\right)^3\)
\(=\left(\dfrac{x^2+y}{x}\right)^3\)
\(=\dfrac{x^6+3x^4y+3x^2y^3+y^3}{x^3}\)
f) \(\left(x-\dfrac{1}{2}\right)^3\)
\(=x^3-3\cdot x^2\cdot\dfrac{1}{2}+3\cdot x\cdot\left(\dfrac{1}{2}\right)^2-\left(\dfrac{1}{2}\right)^3\)
\(=x^3-\dfrac{3}{2}x^2+\dfrac{3}{4}x-\dfrac{1}{8}\)
h) \(\left(x+\dfrac{y^2}{2}\right)^3\)
\(=\left(\dfrac{2x}{2}+\dfrac{y^2}{2}\right)^3\)
\(=\left(\dfrac{2x+y^2}{2}\right)^3\)
\(=\dfrac{8x^3+12x^2y^2+6xy^4+y^6}{8}\)
k) \(\left(x-\dfrac{1}{3}\right)^3\)
\(=x^3-3\cdot x^2\cdot\dfrac{1}{3}+3\cdot x\cdot\left(\dfrac{1}{3}\right)^2-\left(\dfrac{1}{3}\right)^3\)
\(=x^3-x^2+\dfrac{x}{3}-\dfrac{1}{27}\)
m) \(\left(x+\dfrac{y^2}{3}\right)^3\)
\(=\left(\dfrac{3x}{3}+\dfrac{y^2}{3}\right)^3\)
\(=\left(\dfrac{3x+y^2}{3}\right)^3\)
\(=\dfrac{27x^3+27x^2y^2+9xy^4+y^6}{27}\)
Q) \(2\left(x^2+\dfrac{1}{2}y\right)\left(2x^2-y\right)\)
\(=2\left(2x^4-x^2y+x^2y-\dfrac{1}{2}y^2\right)\)
\(=2\left(2x^4-\dfrac{1}{2}y^2\right)\)
\(=4x^4-y^2\)
TN
3
HN
2 tháng 4 2021
a) (Bạn tự vẽ hình ạ)
Ta có AD.AB = AE.AC
⇒ \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta ABC\) và \(\Delta AED\) có:
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
\(\widehat{A}:chung\)
⇒ \(\Delta ABC\sim\Delta AED\) \(\left(c.g.c\right)\)
⇒ DE // BC
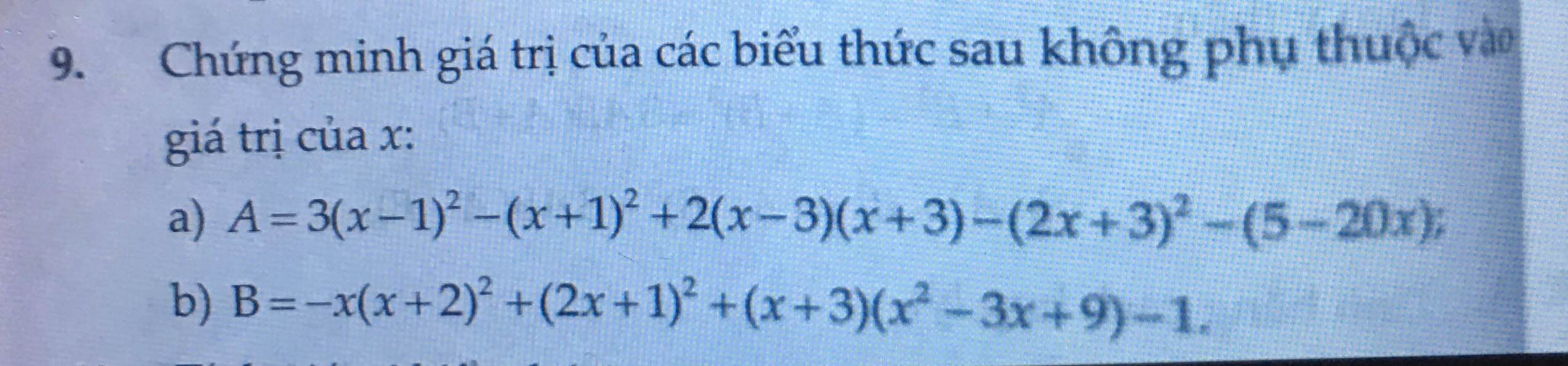
xy + y2 - x - y
= (xy - x) + (y2-y)
= x(y - 1) + y(y - 1)
= (y - 1)(x + y)