Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\overrightarrow {FM} = \left( {x - \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} \)
\(d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|\)
b) M thuộc parabol (P) nên M cách đều F và \(\Delta \)
Suy ra \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x - \frac{p}{2}} \right|\)

Ta có: \(M{F_1} = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} ,M{F_2} = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \).Vậy để điểm M thuộc Hyperbol khi và chỉ khi \(\left| {M{F_1} - M{F_2}} \right| = 2a\) hay\(\left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)

a) Tọa độ 2 tiêu điểm là: \({F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right)\).
b) Ta có: \(M{F_1} = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} ,M{F_2} = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \).Vậy để điểm M thuộc Elip thì khoảng cách\(M{F_1} + M{F_2} = 2a\) nên \(\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} = 2a\)

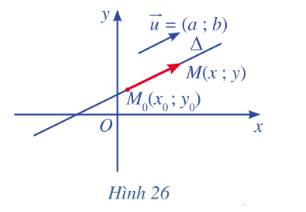
a) Hai vectơ \(\overrightarrow u {\rm{ }}\)và \(\overrightarrow {{M_o}M} \)cùng phương với nhau.
b) Xét \(M\left( {x;y} \right)\). Vì cùng phương với nên có số thực t sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }}\)
c) Do \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\) nên:
\(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }} \Leftrightarrow \left\{ \begin{array}{l}x - {x_o} = at\\y - {y_o} = bt\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = {x_o} + at\\y = {y_o} + bt\end{array} \right.\)
Vậy tọa độ điểm M là: \(M\left( {{x_o} + at;{y_o} + bt} \right)\)

a) Do MH vuông góc với đường thẳng \(\Delta \) nên ta có vecto chỉ phương của MH là: \(\overrightarrow u = \left( {2;1} \right)\)
b) Phương trình tham số của đường thẳng MH đi qua \(M\left( { - 1;1} \right)\) có vecto chỉ phương\(\overrightarrow u = \left( {2;1} \right)\) là: \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 1 + t\end{array} \right. \Leftrightarrow x - 2y + 3 = 0\)
c) H là giao điểm của MH và đường thẳng \(\Delta \)
Xét hệ phương trình: \(\left\{ \begin{array}{l}x - 2y + 3 = 0\\2x + y - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\) . Vậy tọa độ điểm H là: \(H\left( {1;2} \right)\)
Độ dài đoạn thẳng MH là: \(MH = \sqrt {{{\left( {1 + 1} \right)}^2} + {{\left( {2 - 1} \right)}^2}} = \sqrt {{2^2} + {1^2}} = \sqrt 5 \)

a) (E) có tiêu điểm \({F_1}\left( { - \sqrt 3 ;0} \right)\) nên \(c = \sqrt 3\).
Phương trình chính tăc của (E) có dạng
\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)
Ta có: \(M\left( {1;{{\sqrt 3 } \over 2}} \right) \in (E)\)
\(\Rightarrow {1 \over {{a^2}}} + {3 \over {4{b^2}}} = 1\ (1)\)
Và \({a^2} = {b^2} + {c^2} = {b^2} + 3\)
Thay vào (1) ta được :
\(\eqalign{ & {1 \over {{b^2} + 3}} + {3 \over {4{b^2}}} = 1 \cr & \Leftrightarrow 4{b^2} + 3{b^2} + 9 = 4{b^2}(b + 3) \cr}\)
\(\Leftrightarrow 4{b^4} + 5{b^2} - 9 = 0 \Leftrightarrow {b^2} = 1\)
Suy ra \({a^2} = 4\)
Ta có a = 2 ; b = 1.
Vậy (E) có bốn đỉnh là : (-2 ; 0), (2 ; 0)
(0 ; -1) và (0 ; 1).
b) Phương trình chính tắc của (E) là :
\({{{x^2}} \over 4} + {{{y^2}} \over 1} = 1\)
c) (E) có tiêu điểm thứ hai là điểm \(\left( {\sqrt 3 ;0} \right)\). Đường thẳng \(\Delta\) đi qua điểm\(\left( {\sqrt 3 ;0} \right)\) và vuông góc với Ox có phương trình \(x = \sqrt 3\).
Phương trình tung độ giao điểm của \(\Delta\) và \((E)\) là :
\({3 \over 4} + {{{y^2}} \over 1} = 1 \Leftrightarrow {y^2} = \pm {1 \over 2}\)
Suy ra tọa độ của C và D là :
\(C\left( {\sqrt 3 ; - {1 \over 2}} \right)\) và \(\left( {\sqrt 3 ;{1 \over 2}} \right)\)
Vậy CD = 1.

a) Tọa độ vecto pháp tuyến của \(\Delta \) là:
Tọa độ vecto chỉ phương của \(\Delta \) là:
b) Chọn \(x = 0;x = 1\) ta lần được được 2 điểm A và B thuộc đường thẳng \(\Delta \) là: \(A\left( {0;1} \right),B\left( {1;2} \right)\)

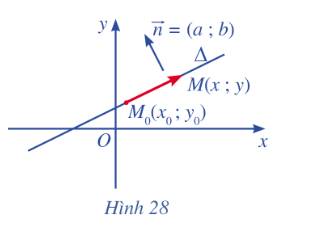
a) Phương của hai vecto \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \) vuông góc với nhau.
b) Ta có: \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\)
Xét điểm \(M\left( {x;y} \right) \in \Delta \). Vì \(\overrightarrow {{M_o}M} \bot \overrightarrow n \) nên: \(\overrightarrow {{M_o}M} .\overrightarrow n = 0 \Leftrightarrow a\left( {x - {x_o}} \right) + b\left( {y - {y_o}} \right) = 0 \Leftrightarrow ax + by - a{x_o} + b{y_o} = 0\)
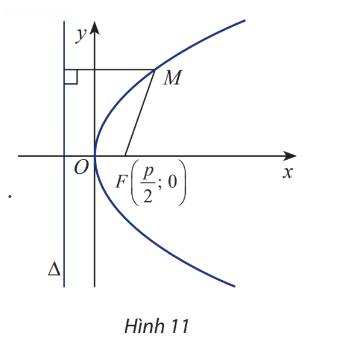
a) Tọa độ điểm F là: \(F\left( {\frac{p}{2};0} \right)\) và phương trình đường chuẩn là: \(\Delta :x = - \frac{p}{2}\)
b) Ta có: \(MF = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} ,d\left( {M,\Delta } \right) = \left| {x + \frac{p}{2}} \right|\). Để M thuộc (P) thì \(MF{\rm{ }} = \;d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\)