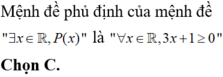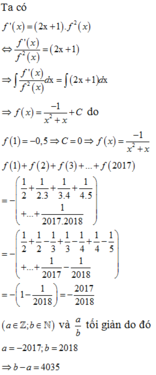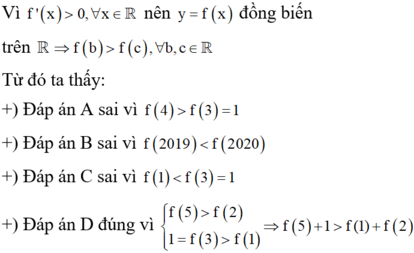Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Dựa vào giả thiết, ta thấy rằng:
log 2 x − 1 2 + 2 log 2 x + 1 = 6 ⇔ 2 log 2 x − 1 + 2 log 2 x + 1 = 6 ⇒ 1 s a i .
x 2 + 1 ≥ 2 x ⇔ log 2 x 2 + 1 ≥ log 2 2 x = 1 + log 2 x ; ∀ x ∈ ℝ ⇒ 2 đ ú n g
x ln y = y ln x ; ∀ x > y > 2 ⇒ 3 đúng.
log 2 2 2 x − 4 log 2 x − 4 = 0 ⇔ log 2 x + 1 2 − 4 log 2 x − 4 = 0 ⇔ log 2 2 − 2 log 2 x − 3 = 0
⇒ 4 sai. Vậy có 2 mệnh đề đúng

Đáp án C
Mệnh đề (I) đúng.
Mệnh đề (II) sai vì log 3 x 2 = 2 log 3 x khi x > 0 nên điều kiện ∀ x ∈ ℝ \ 0 là chưa đủ.
Mệnh đề (III) sai vì log a b . c = log a b + log a c
Số mệnh đề đúng là 1.

Đáp án B
Mệnh đề 1) sai vì: log 2 x − 1 2 = 2 log 2 x − 1
Mệnh đề 2) sai vì khi x=0 biểu thức vế trái không xác định.
Mệnh đề 3) đúng vì với x > y > 2 ta luôn có:
ln x . ln y = ln y . ln x ⇔ ln x ln y = ln y ln x ⇔ x ln y = y ln x
Mệnh đề 4) sai vì:
log 2 2 2 x − 4 log 2 x − 4 = 0 ⇔ 1 + log 2 x 2 − 4 log 2 x − 4 = 0 ⇔ log 2 2 x − 2 log 2 x − 3 = 0

Chọn đáp án C

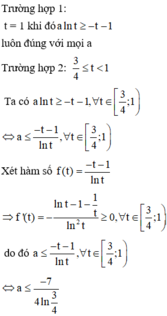
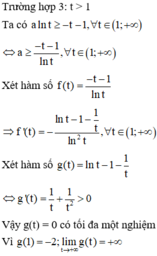
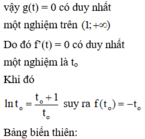
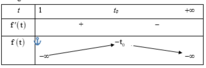

Vậy số thực a thỏa mãn yêu cầu bài toán là: a ∈ ( 6 ; 7 ]