Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

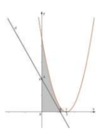

Phương trình đường thẳng(d) có hệ số góc k và cắt trục tung tại điểm A (0;4) là: y = kx +4

Đáp án A

Câu 3:
Phương trình hoành độ giao điểm:
\(x^3=x^2-4x+4\Leftrightarrow x^3-x^2+4x-4=0\Rightarrow x=1\)
\(x^3=0\Rightarrow x=0\)
\(x^2-4x+4=0\Rightarrow x=2\)
Diện tích hình phẳng:
\(S=\int\limits^1_0x^3dx+\int\limits^2_1\left(x^2-4x+4\right)dx=\frac{7}{12}\)
Câu 4:
Phương trình hoành độ giao điểm:
\(x^3-3x+2=x+2\Leftrightarrow x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=0\\x=2\end{matrix}\right.\)
Diện tích hình phẳng:
\(S=\int\limits^0_{-2}\left(x^3-3x+2-x-2\right)dx+\int\limits^2_0\left(x+2-x^3+3x-2\right)dx=8\)
Câu 1:
Phương trình hoành độ giao điểm: \(cosx=0\Rightarrow x=\frac{\pi}{2}\)
\(\Rightarrow S=\int\limits^{\frac{\pi}{2}}_0cosxdx-\int\limits^{\pi}_{\frac{\pi}{2}}cosxdx=2\)
Câu 2:
Phương trình hoành độ giao điểm: \(x.e^x=0\Rightarrow x=0\)
\(\Rightarrow S=\int\limits^3_0xe^x-\int\limits^0_{-2}xe^xdx\)
Xét \(I=\int x.e^xdx\Rightarrow\left\{{}\begin{matrix}u=x\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=x.e^x-\int e^xdx=xe^x-e^x+C=\left(x-1\right)e^x+C\)
\(\Rightarrow S=\left(x-1\right)e^x|^3_0-\left(x-1\right)e^x|^0_{-2}=2e^3+1-\left[-1+\frac{3}{e^2}\right]=2e^3+2-\frac{3}{e^2}\)

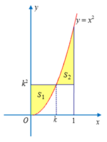
Phương trình đường thẳng d đi qua A(0;4) có hệ số góc k

Vì d chia (H) thành 2 phần có diện tích bằng nhau
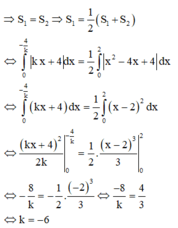
Đáp án A

Câu 1:
\(\overrightarrow{MN}=\left(3;-1;-4\right)\Rightarrow\) pt mặt phẳng trung trực của MN:
\(3\left(x-\frac{7}{2}\right)-\left(y-\frac{1}{2}\right)-4\left(z-2\right)=0\Leftrightarrow3x-y-4z-2=0\)
\(\overrightarrow{PN}=\left(4;3;-1\right)\Rightarrow\) pt mp trung trực PN: \(4x+3y-z-7=0\)
\(\Rightarrow\) Phương trình đường thẳng giao tuyến của 2 mp trên: \(\left\{{}\begin{matrix}x=1+t\\y=1-t\\z=t\end{matrix}\right.\)
\(\Rightarrow I\left(1+c;1-c;c\right)\) \(\Rightarrow\overrightarrow{NI}=\left(c-4;1-c;c\right)\)
\(d\left(I;\left(Oyz\right)\right)=IN\Rightarrow\left|1+c\right|=\sqrt{\left(c-4\right)^2+\left(1-c\right)^2+c^2}\)
\(\Leftrightarrow\left(c+1\right)^2=3c^2-10c+17\)
\(\Leftrightarrow2c^2-12c+16=0\Rightarrow\left[{}\begin{matrix}c=4\\c=2\end{matrix}\right.\)
Mà \(a+b+c< 5\Rightarrow\left(1+c\right)+\left(1-c\right)+c< 5\Rightarrow c< 3\Rightarrow c=2\)
Câu 2:
Phương trình tham số d: \(\left\{{}\begin{matrix}x=-1+2t\\y=t\\z=2-t\end{matrix}\right.\) \(\Rightarrow C\left(-1+2n;n;2-n\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(2n;n-3;1-n\right)\\\overrightarrow{AB}=\left(1;-1;-2\right)\end{matrix}\right.\) \(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(3n-7;-3n-1;3n-3\right)\)
\(\Rightarrow S_{ABC}=\frac{1}{2}\left|\left[\overrightarrow{AB};\overrightarrow{AC}\right]\right|=2\sqrt{2}\)
\(\Leftrightarrow\sqrt{\left(3n-7\right)^2+\left(-3n-1\right)^2+\left(3n-3\right)^2}=4\sqrt{2}\)
\(\Leftrightarrow27n^2-54n+27=0\Rightarrow n=1\)
\(\Rightarrow C\left(1;1;1\right)\Rightarrow m+n+p=3\)

Lời giải:
Ta có:
\(y=\frac{k\sin x+1}{\cos x+2}\Rightarrow y\cos x+2y=k\sin x+1\)
\(\Leftrightarrow 2y-1=k\sin x-y\cos x\)
Theo BĐT Bunhiacopxky:
\((2y-1)^2=(k\sin x-y\cos x)^2\leq (k^2+y^2)(\sin ^2x+\cos ^2x)=k^2+y^2\)
\(\Leftrightarrow 4y^2-4y+1\leq k^2+y^2\)
\(\Leftrightarrow 3y^2-4y+1\leq k^2\)
\(\Leftrightarrow 3(y-\frac{2}{3})^2\leq k^2+\frac{1}{3}\)
\(\Leftrightarrow \frac{2}{3}-\sqrt{\frac{3k^2+1}{9}}\leq y\leq \frac{2}{3}+\sqrt{\frac{3k^2+1}{9}}\)
\(\Rightarrow y_{\min}=\frac{2}{3}-\sqrt{\frac{3k^2+1}{9}}\)
Để \(y_{\min}< -1\Leftrightarrow \sqrt{\frac{3k^2+1}{9}}>\frac{5}{3}\Leftrightarrow k^2>8\Leftrightarrow \left[\begin{matrix} k>2\sqrt{2}\\ k<-2\sqrt{2}\end{matrix}\right.\)
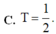
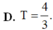
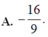
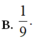
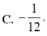
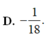


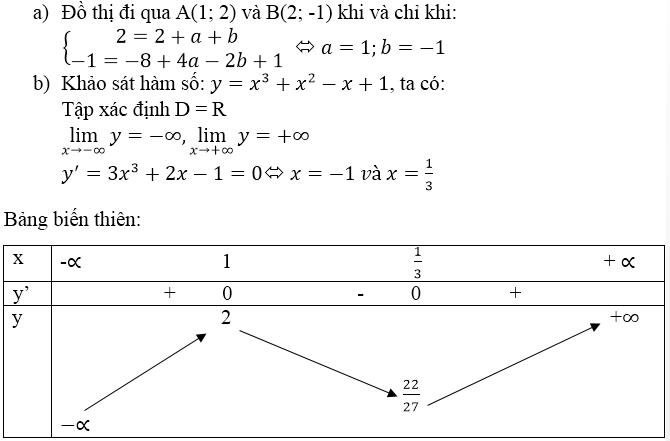
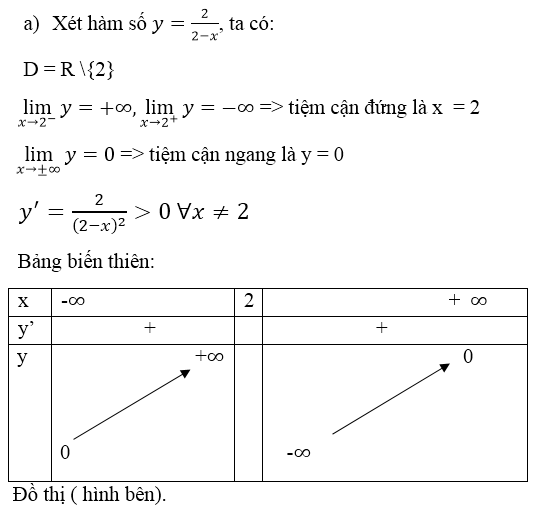

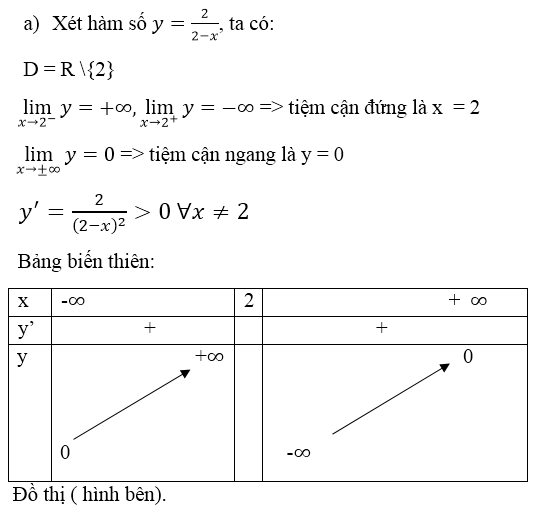
Đáp án B.