
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

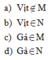

Q là tập hợp các số hữu tỉ
N là tập hợp các số tự nhiên
\(83\in Q\) \(;91\in Q\) \(;15\in N\) \(;Q\supset E\) ( Có thể điền giá trị khác )
K mk nha, mk sẽ k bạn

1, Ta có: A = { 0; 1; 2; 3; 4; 5; 6 }
B = { 3; 4; 5 }
C = { 1; 2; 3; ... }
D = \(\varnothing\)
G = \(\varnothing\)
H = { 9; 10; 11; 12; 13; 14; 15 }
2, Ta có: E \(\subset\) C
3, Vì không có phần tử nào thuộc tập hợp G
Nên tổng các phần tử của hai tập hợp E và G bằng tổng các phần tử của tập hợp E
=> Tổng các phần tử của tập hợp E và G là:
[ ( 99 - 10 ) : 1 + 1 ]( 99 + 10 ) : 2 = 90 . 109 : 2 = 4905

x y O m n 56 độ
a, Vì \(\widehat{xOm}\) và \(\widehat{yOn}\) phụ nhau nên ta có:
\(\widehat{xOm}+\widehat{yOn}=90^o\)
\(56^o+\widehat{yOn}=90^o\)
\(\widehat{yOn}=90^o-56^o\)
\(\widehat{yOn}=34^o\)
b, Vì \(\widehat{xOm}\) và \(\widehat{yOm}\) kề bù nên ta có:
\(\widehat{xOm}+\widehat{yOm}=180^o\)
\(56^o+\widehat{yOm}=180^o\)
\(\widehat{yOm}=180^o-56^o\)
\(\widehat{yOm}=124^o\)
c, Vì \(\widehat{yOn}\) và \(\widehat{xOn}\) kề bù nên ta có:
\(\widehat{yOn}+\widehat{xOn}=180^o\)
\(34^o+\widehat{xOn}=180^o\)
\(\widehat{xOn}=180^o-34^o\)
\(\widehat{xOn}=146^o\)