K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
19 tháng 2 2018
Chọn C.
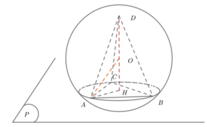
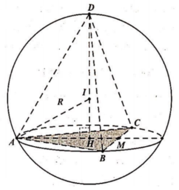
Phương pháp: Tìm vị trí điểm D để thể tích ABCD lớn nhất.

CM
4 tháng 1 2020
Đáp án là B

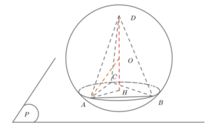
Gọi K là trọng tâm tam giác ABC, N đỗi xứng với D qua J, qua K kẻ KO song song với DN ta có O là tâm mặt cầu cần xác định.
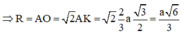

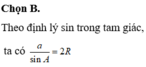






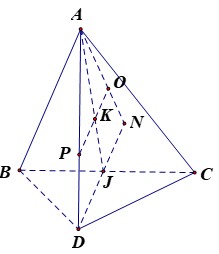
Đáp án B
Áp dụng công thức tính diện tích tam giác S = p . r trong đó p là nửa chu vi và r là bán kính đường tròn nội tiếp tam giác
Đặt A B = A C = a , B C = b a , b > 0
Ta có: S A B C = p . r = p .1 = p = a + a + b 2 = a + b 2
Kẻ đường cao AH ta có: b 2 = a sin A 2 ⇒ S A B C = a + a sin A 2
Ta lại có S A B C = 1 2 a 2 sin A = a + a sin A 2 = a 1 + sin A 2
⇒ 1 2 a sin A = 1 + sin A 2 ⇔ a = 2 1 + sin A 2 sin A
⇒ S A B C = 2 1 + sin A 2 2 sin A 0 < A < π
Dùng M O D E 7 tìm GTNN của hàm số trên ta nhận được: