Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
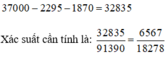
Chọn D

Đáp án C
Số cách xếp ngẫu nhiên là 10!.
Ta tìm số cách xếp thoả mãn:
Đánh số hàng từ 1 đến 10. Có hai khả năng:
5 nam xếp vị trí lẻ và 5 nữ xếp vị trí chẵn có 5! x 5! = 120 2 .
5 nam xếp vị trí chẵn và 5 nữ xếp vị trí lẻ có 5! x 5! = 120 2 .
Theo quy tắc cộng có 120 2 + 120 2 = 2 × 120 2 cách xếp thoả mãn.
Vậy xác suất cần tính 2 5 ! 2 10 ! = 1 126 .

Đáp án B
Số phần tử KGM là: 9!. Mà số phần tử của biến cố các học sinh nữ luôn ngồi cạnh nhau là: 3!7!
Xác suất để các học sinh nữ luôn ngồi cạnh nhau là: 3!7! 9! = 1 12

Đáp án C
Xếp 3 khối có 3! cách.
Xếp 5 học sinh lớp 10 có 5! cách.
Xếp 6 học sinh lớp 11 có 6! cách.
Xếp 7 học sinh lớp 12 có 7! cách.
Vậy có cách xếp.

Đáp án B

Số cách xếp 10 học sinh vào 10 ghế là: 10!
4 bạn nữ chỉ có thể xếp vào các vị trí N1,N2,N3,N4
Nếu Huyền ở vị trí N1 thì có 3! cách xếp 3 bạn nữ còn lại, Quang có 5 cách chọn chỗ ngồi và có 5! cách xếp 5 bạn nam còn lại. Vậy có 3!.5.5! = 3600 cách xếp
Tương tự nếu Huyền ở vị trí N4 cũng có 3600 cách xếp
Nếu Huyền ở vị trí N2 thì có 3! cách xếp 3 bạn nữ còn lại, Quang có 4 cách chọn chỗ ngồi và có 5! cách xếp 5 bạn nam còn lại. Vậy có 3!.4.5! = 2880 cách xếp
Tương tự nếu Huyền ở vị trí N3 cũng có 2880 cách xếp
Vậy có 2(3600 + 2880) = 12960 cách xếp thỏa mãn đề bài
⇒ p = 12960 10 ! = 1 280




Đáp án D
“Xếp 11 học sinh nữa thành 1 hàng dọc” Số phần tử không gian mẫu n Ω = 11 !
A:"2 học sinh nữ bất kỳ không xếp cạnh nhau "
Có 7! Cách sắp xếp các học sinh nam thành 1 hàng:1N2N3N4N5N6N7N8
Khi đó có 8 vị trí xen kẽ các học sinh nam.
Để 2 học sinh nữ bất kỳ không xếp cạnh nhau ta sắp xếp 4 học sinh nữ vào 8 vị trí này có A 8 4 cách sắp xếp. ⇒ n A = 7 ! . A 8 4 . Vậy P A = 7 ! . A 8 4 . 11 !