K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KV
25 tháng 5 2023
x⁸ + x⁴ + 1
= x⁸ + 2x⁴ + 1 - x⁴
= (x⁴ + 1)² - x⁴
= (x⁴ + 1)² - (x²)²
= (x⁴ + 1 + x²)(x⁴ + 1 - x²)
= (x⁴ + x² + 1)(x⁴ - x² + 1)
31 tháng 7 2021
19) Ta có: \(-x^2-4x-4\)
\(=-\left(x^2+4x+4\right)\)
\(=-\left(x+2\right)^2\)
20) Ta có: \(-4x^2-12x-9\)
\(=-\left(4x^2+12x+9\right)\)
\(=-\left(2x+3\right)^2\)
21) Ta có: \(-4x^2-4x-1\)
\(=-\left(4x^2+4x+1\right)\)
\(=-\left(2x+1\right)^2\)
22) Ta có: \(-x^2+6x-9\)
\(=-\left(x^2-6x+9\right)\)
\(=-\left(x-3\right)^2\)
23) Ta có: \(-x^2+10x-25\)
\(=-\left(x^2-10x+25\right)\)
\(=-\left(x-5\right)^2\)
24) Ta có: \(-x^2+8x-16\)
\(=-\left(x^2-8x+16\right)\)
\(=-\left(x-4\right)^2\)
25) Ta có: \(-4x^2+12x-9\)
\(=-\left(4x^2-12x+9\right)\)
\(=-\left(2x-3\right)^2\)
26) Ta có: \(a^2-a+b-b^2\)
\(=\left(a-b\right)\left(a+b\right)-\left(a-b\right)\)
\(=\left(a-b\right)\left(a+b-1\right)\)
31 tháng 7 2021
13) Ta có: \(y^2-2xy+2x-y\)
\(=y\left(y-2x\right)-\left(y-2x\right)\)
\(=\left(y-2x\right)\left(y-1\right)\)
14) Ta có: \(x-2xy+4y-2\)
\(=x\left(1-2y\right)-2\left(1-2y\right)\)
\(=\left(1-2y\right)\left(x-2\right)\)
15) Ta có: \(x^2-2xy+x-2y\)
\(=x\left(x-2y\right)+\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x+1\right)\)
16) Ta có: \(xy-z-y+xz\)
\(=x\left(y+z\right)-\left(y+z\right)\)
\(=\left(y+z\right)\left(x-1\right)\)
17) Ta có: \(2xy+3z-6y-xz\)
\(=\left(2xy-xz\right)+\left(3z-6y\right)\)
\(=x\left(2y-z\right)-3\left(2y-z\right)\)
\(=\left(2y-z\right)\left(x-3\right)\)
18) Ta có: \(2xy-2z+4y-xz\)
\(=\left(2xy+4y\right)+\left(xz+2z\right)\)
\(=2y\left(x+2\right)+z\left(x+2\right)\)
\(=\left(x+2\right)\left(2y+z\right)\)
8 tháng 8 2021
26) Ta có: \(x^4-20x^2+64\)
\(=x^4-16x^2-4x^2+64\)
\(=x^2\left(x^2-16\right)-4\left(x^2-16\right)\)
\(=\left(x-4\right)\left(x+4\right)\left(x-2\right)\left(x+2\right)\)
27) Ta có: \(4x^3+6x^2+3x+1\)
\(=4x^3+4x^2+2x^2+2x+x+1\)
\(=4x^2\left(x+1\right)+2x\left(x+1\right)+\left(x+1\right)\)
\(=\left(x+1\right)\left(4x^2+2x+1\right)\)
28) Ta có: \(x^3-6x^2+12x-9\)
\(=x^3-3x^2-3x^2+9x+3x-9\)
\(=x^2\cdot\left(x-3\right)-3x\left(x-3\right)+3\left(x-3\right)\)
\(=\left(x-3\right)\left(x^2-3x+3\right)\)
29: Ta có: \(x^4+x^2+1\)
\(=x^4+2x^2+1-x^2\)
\(=\left(x^2+1\right)^2-x^2\)
\(=\left(x^2-x+1\right)\left(x^2+x+1\right)\)
HN
9 tháng 8 2021
26) Ta có: x4−20x2+64x4−20x2+64
=x4−16x2−4x2+64=x4−16x2−4x2+64
=x2(x2−16)−4(x2−16)=x2(x2−16)−4(x2−16)
=(x−4)(x+4)(x−2)(x+2)=(x−4)(x+4)(x−2)(x+2)
27) Ta có: 4x3+6x2+3x+14x3+6x2+3x+1
=4x3+4x2+2x2+2x+x+1=4x3+4x2+2x2+2x+x+1
=4x2(x+1)+2x(x+1)+(x+1)=4x2(x+1)+2x(x+1)+(x+1)
=(x+1)(4x2+2x+1)=(x+1)(4x2+2x+1)
28) Ta có: x3−6x2+12x−9x3−6x2+12x−9
=x3−3x2−3x2+9x+3x−9=x3−3x2−3x2+9x+3x−9
=x2⋅(x−3)−3x(x−3)+3(x−3)=x2⋅(x−3)−3x(x−3)+3(x−3)
=(x−3)(x2−3x+3)=(x−3)(x2−3x+3)
29: Ta có: x4+x2+1x4+x2+1
=x4+2x2+1−x2=x4+2x2+1−x2
=(x2+1)2−x2=(x2+1)2−x2
=(x2−x+1)(x2+x+1)
NT
3
H
6 tháng 9 2023
\(\left(a-b\right)^2-\left(b-a\right)\\ =\left(a-b\right)\left(a-b\right)+\left(a-b\right)\\ =\left(a-b\right)\left(a-b+1\right)\)
`HaNa☘D`
KV
6 tháng 9 2023
\(\left(a-b\right)^2-\left(b-a\right)\)
\(=\left(a-b\right)^2+\left(a-b\right)\)
\(=\left(a-b\right)\left(a-b+1\right)\)
24 tháng 8 2023
=(x-y-2y)[(x-y)^2+2y(x-y)+4y^2]
=(x-3y)(x^2-2xy+y^2+2xy-2y^2+4y^2)
=(x-3y)(x^2+3y^2)
H9
HT.Phong (9A5)
CTVHS
24 tháng 8 2023
\(\left(x-y\right)^3-8y^3\)
\(=\left(x-y\right)^3-\left(2y\right)^3\)
\(=\left[\left(x-y\right)-2y\right]\left[\left(x-y\right)^2+2y\left(x-y\right)+\left(2y\right)^2\right]\)
\(=\left(x-y-2y\right)\left(x^2-2xy+y^2+2xy-2y^2+4y^2\right)\)
\(=\left(x-3y\right)\left(x^2+3y^2\right)\)
H
24 tháng 8 2023
\(\left(x-y\right)^3-\left(x+y\right)^3\\ =\left(x-y-x-y\right)\left(\left(x-y\right)^2+\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\right)\\ =-2y\left(x^2-2xy+y^2+x^2-y^2+x^2+2xy+y^2\right)\\ =-2y\left(3x^2+y^2\right)\)
H
24 tháng 8 2023
\(\left(x-y\right)^3+\left(x+y\right)^3\\ =\left(x-y+x+y\right)\left(\left(x-y\right)^2-\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\right)\\ =2x\left(x^2-2xy+y^2-\left(x^2-y^2\right)+x^2+2xy+y^2\right)\\ =2x\left(x^2-2xy+y^2-x^2+y^2+x^2+2xy+y^2\right)\\ =2x\left(x^2+3y^2\right)\)
PL
2
T
25 tháng 8 2023
\(3x\cdot\left(x-y\right)^2-6\cdot\left(y-x\right)\)
\(=3x\left(x-y\right)^2+6\left(x-y\right)\)
\(=\left(x-y\right)\left[3x\left(x-y\right)+6\right]\)
\(=\left(x-y\right)\left(3x^2-3xy+6\right)\)
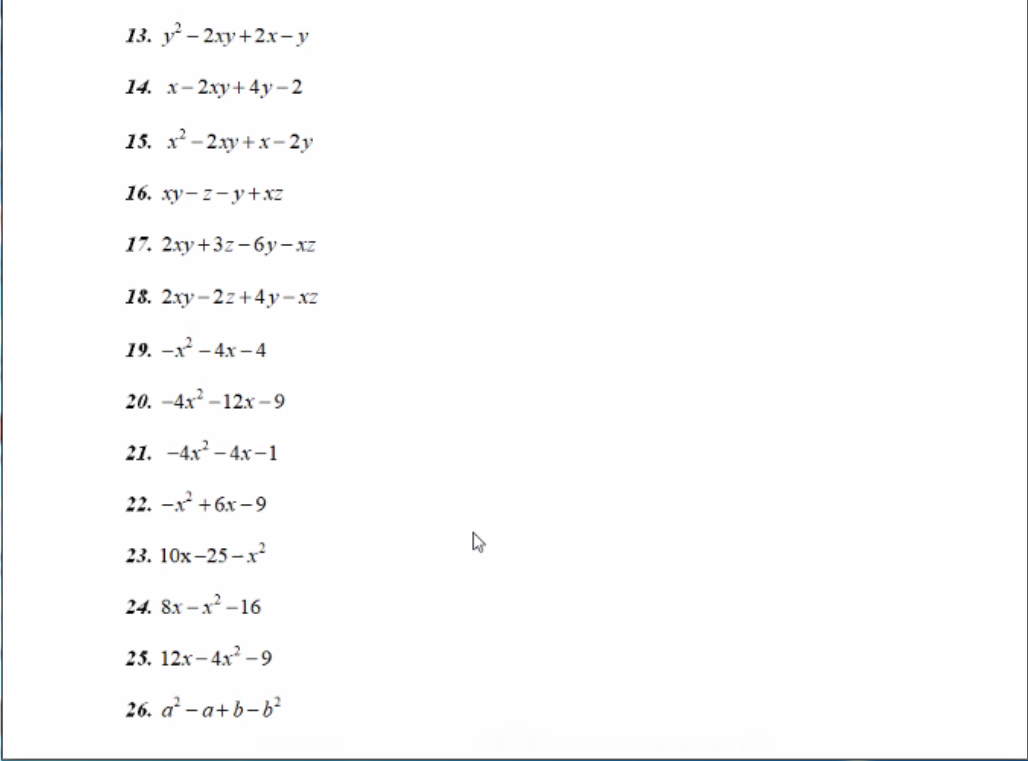
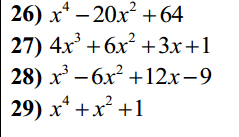
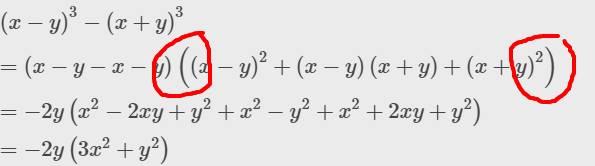
\(x^2-y^2\)
\(=x^2+xy-xy-y^2\)
\(=x\left(x+y\right)-y\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y\right)\)
x²-y²=(x+y)(x-y)