Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì \(f\left(b\right)\) đồng biến nên nếu \(f\left(-8\right)>0\Rightarrow f\left(b\right)>0;\forall b>-8\)
\(\Rightarrow f\left(b\right)\le0\) có nhiều nhất 3 nghiệm nguyên thuộc (-12;12) là -11;-10;-9 (ktm yêu cầu đề bài)
Do đó \(f\left(-8\right)\le0\)
Hiểu đơn giản thì đếm từ -11 trở đi thêm 4 số nguyên ta sẽ chạm tới mốc -8

Lời giải:
Áp dụng BĐT Cô-si:
\(2=a+b=\frac{a}{2}+\frac{a}{2}+b\geq 3\sqrt[3]{\frac{a^2b}{4}}\)
\(\Rightarrow \frac{2}{3}\geq \sqrt[3]{\frac{a^2b}{4}}\Rightarrow \frac{8}{27}\geq \frac{a^2b}{4}\)
\(\Leftrightarrow a^2b\leq \frac{32}{27}\Leftrightarrow P\leq \frac{32}{27}\)
Vậy $P_{\max}=\frac{32}{27}$. Giá trị này đạt tại $\frac{a}{2}=b=\frac{2}{3}$
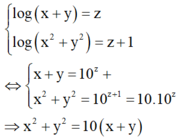
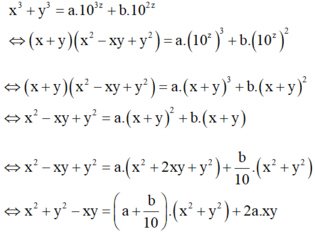

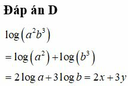




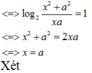
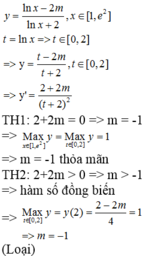
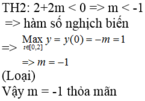
Đây là trắc nghiệm đúng không. Vậy thì 4 đáp án a,b,c,d đâu rồi. Không thể tính ra số cụ thể đâu. Nhưng có thể biểu diễn theo biến.
Giả thiết của đề bài như bị thiếu.