Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(n\left(5n-2\right)-5n\left(n+3\right)\)
\(=n\left(5n-2\right)-n\left(5n+3\right)\)|
\(=n\left(5n-2-5n-3\right)=-5n\) ; Vì \(n\in Z\)
\(\Rightarrow-5n\in Z\Rightarrow
-5n⋮-5\)
Vậy: .......
#HọcTốt!!

n(4n-1)-4n(n+2)=4n2-n-4n2-8n=-9n
=>n(4n-1)-4n(n+2) luôn chia hết cho 9

n( 3n - 2 ) - 3n( n + 2 )
= 3n2 - 2n - 3n2 - 6n
= -8n luôn chia hết cho ±1 ; ±2 ; ±4 ; ±8

a: \(n^3-2⋮n-2\)
=>\(n^3-8+6⋮n-2\)
=>\(6⋮n-2\)
=>\(n-2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(n\in\left\{3;1;4;0;5;-1;8;-4\right\}\)
b: \(n^3-3n^2-3n-1⋮n^2+n+1\)
=>\(n^3+n^2+n-4n^2-4n-4+3⋮n^2+n+1\)
=>\(3⋮n^2+n+1\)
=>\(n^2+n+1\in\left\{1;-1;3;-3\right\}\)
mà \(n^2+n+1=\left(n+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall n\)
nên \(n^2+n+1\in\left\{1;3\right\}\)
=>\(\left[{}\begin{matrix}n^2+n+1=1\\n^2+n+1=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}n^2+n=0\\n^2+n-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}n\left(n+1\right)=0\\\left(n+2\right)\left(n-1\right)=0\end{matrix}\right.\Leftrightarrow n\in\left\{0;-1;-2;1\right\}\)

5n^3 + 15n^2 +10n
=(5n^3 + 15n^2+ 10n)
= 30n^6 chia hết cho 30
Ta có : 5n3+15n2+10n
=5n(n2+3n+2)
Ta thấy : 5 chia hết cho 30
Hay : 5n chia hết cho 30
Vậy đpcm

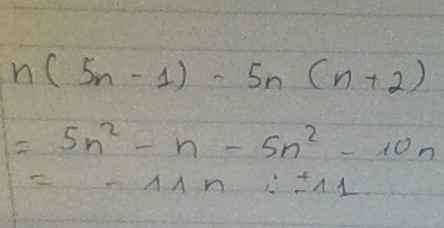
\(n\left(5n-1\right)-5n\left(n+2\right)=5n^2-n-5n^2-10n=-11n⋮11\forall n\in Z\)