Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Với những giá trị nào của x thì giá trị của hai biểu thức sau bằng nhau? -2 2 x – 1 và 2 x 2 + 2x +3

Ta có: -2 2 x – 1 = 2 x 2 + 2x +3 ⇔ 2 x 2 +2x + 3 + 2 2 x + 1=0
⇔ 2 x 2 + 2(1 + 2 )x +4 =0
∆ ' = b ' 2 – ac= 1 + 2 2 - √2 .4= 1+2 2 +2 - 4 2
= 1-2 2 +2 = 2 - 1 2 > 0
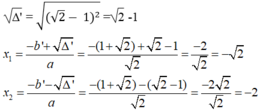
Vậy với x= - 2 hoặc x = -2 thì giá trị của hai biểu thức trên bằng nhau

Ta có: 3 x 2 + 2x -1 = 2 3 x + 3 ⇔ 3 x 2 + 2x - 2 3 x -3 -1 = 0
⇔ 3 x 2 + (2 - 2 3 )x -4 =0 ⇔ 3 x 2 + 2(1 - 3 )x -4 = 0
∆ ' = b ' 2 – ac= 1 - 3 2 - 3 (-4) =1 - 2 3 +3 +4 3
= 1 + 2 3 +3 = 1 - 3 2 > 0
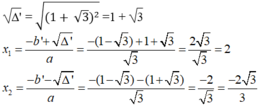
Vậy với x= 2 hoặc x = (-2 3 )/3 thì giá trị của hai biểu thức trên bằng nhau

Ta có: x 2 - 2 3 x - 3 = 2 x 2 +2x + 3
⇔ x 2 - 2 3 x - 3 - 2 x 2 -2x - 3 =0
⇔ x 2 +2x +2 3 x +2 3 =0
⇔ x 2 + 2(1 + 3 )x + 2 3 =0
∆ ' = b ' 2 – ac= 1 + 3 2 – 1. 2 3 = 1 + 2 3 + 3 -2 3 = 4 > 0
∆ ' = 4 =2
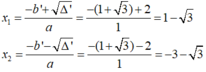
Vậy với x=1 - 3 hoặc x = - 3 - 3 thì giá trị của hai biểu thức trên bằng nhau

Ta có: x 2 +2 + 2 2 = 2(1 + 2 )x ⇔ x 2 - 2(1+ 2 )x +2 +2 2 = 0
∆ ' = b ' 2 – ac = - 1 + 2 2 - 1(2+2 2 )
= 1 + 2 2 +2 -2 -2 2 =1 > 0
∆ ' = 1 =1
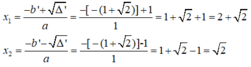
Vậy với x= 2+ 2 hoặc x = 2 thì giá trị của hai biểu thức trên bằng nhau

`a)A=[2\sqrt{3}+2-2\sqrt{3}+2]/[(2\sqrt{3}-2)(2\sqrt{3}+2)]`
`A=4/[12-4]=1/2`
Với `x > 0,x ne 1` có:
`B=[x-2\sqrt{x}+1]/[\sqrt{x}(\sqrt{x}-1)]`
`B=[(\sqrt{x}-1)^2]/[\sqrt{x}(\sqrt{x}-1)]=[\sqrt{x}-1]/\sqrt{x}`
`b)B=2/5A`
`=>[\sqrt{x}-1]/\sqrt{x}=2/5 . 1/2`
`<=>5\sqrt{x}-5=\sqrt{x}`
`<=>\sqrt{x}=5/4`
`<=>x=25/16` (t/m)

b: \(B=\dfrac{x^2-3x+2x^2+6x-3x^2-9}{x^2-9}=\dfrac{3x-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x+3}\)

b: \(B=\dfrac{x^2-3x+2x^2+6x-3x^2-9}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{3x-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x+3}\)

\(P\left(x\right)=\dfrac{4x^4+16x^3+56x^2+80x+356}{x^2+2x+5}\\ P\left(x\right)=\dfrac{4x^2\left(x^2+2x+5\right)+8x\left(x^2+2x+5\right)+20\left(x^2+2x+5\right)+256}{x^2+2x+5}\\ P\left(x\right)=4\left(x^2+2x+5\right)+\dfrac{256}{x^2+2x+5}\\ \ge2\sqrt{\dfrac{4\left(x^2+2x+5\right)\cdot256}{x^2+2x+5}}=2\sqrt{1024}=64\left(BĐTcosi\right)\)
Dấu \("="\Leftrightarrow4\left(x^2+2x+5\right)=\dfrac{256}{x^2+2x+5}\)
\(\Leftrightarrow x^2+2x+5=8\Leftrightarrow x^2+2x-3=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)


Ta có: 3 x 2 + 2 5 x - 3 3 = - x 2 - 2 3 x +2 5 +1
⇔ 3 x 2 + 2 5 x - 3 3 + x 2 + 2 3 x - 2 5 – 1= 0
⇔ ( 3 +1) x 2 + (2 5 + 2 3 )x -3 3 - 2 5 – 1= 0
⇔ ( 3 +1)x2 + 2( 5 + 3 )x -3 3 - 2 5 – 1= 0
∆ ' = b ' 2 – ac= 3 + 5 2 – ( 3 + 1 )( -3 3 - 2 5 – 1)
= 5 + 2 15 +3+9 +2 15 + 3 +3 3 +2 5 + 1
=18 +4 15 +4 3 +2 5
= 1 + 12 + 5 + 2.2 3 + 2 5 + 2.2 3 . 5
= 1 + 2 3 2 + 5 2 + 2.1.2 3 +2.1. 5 + 2.2 5 . 3
= 1 + 2 3 + 5 2 > 0