Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{x^2}{x^2-5x+7}\)
Ta có : \(x^2-5x+7=\left(x-\frac{5}{2}\right)^2+\frac{3}{4}>0\) do đó y xác định với mọi x
\(y=\frac{x^2}{x^2-5x+7}\Leftrightarrow yx^2-5yx+7y=x^2\)
\(\Leftrightarrow\left(y-1\right)x^2-5yx+7y=0\)
* Xét y = 1 ta có : \(-5x+7=0\Leftrightarrow x=\frac{7}{5}\)
* Xét y \(\ne\)1 ta có : \(\Delta=25y^2-28y\left(y-1\right)=25y^2-28y^2+28y\)
\(=-3y^2+28y=y\left(-3y+28\right)\)
Để có x thì phải có \(\Delta\ge0\)
\(\Leftrightarrow\orbr{\begin{cases}y\ge0;-3y+28\ge0\\y\le0;-3y+28\le0\end{cases}\Leftrightarrow\orbr{\begin{cases}y\ge0;y\le\frac{28}{3}\\y\le0;y\ge\frac{28}{3}\end{cases}\Leftrightarrow}0\le y\le\frac{28}{3}}\)
y = 0 thì \(x=\frac{5y}{2\left(y-1\right)}=0\)
y = \(\frac{28}{3}\)thì \(x=\frac{5y}{2\left(y-1\right)}=\frac{14}{5}\)
Vậy : Giá trị nhỏ nhất của y là 0 với x = 0
Giá trị nhỏ nhất của y là \(\frac{28}{3}\) với x = \(\frac{14}{5}\)


Vẽ hình:
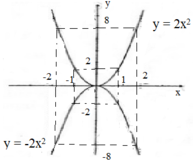
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.


Vẽ hình:
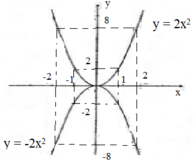
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
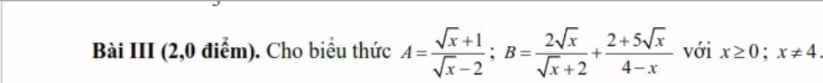
Bài giải
\(A=-5x^2+\frac{10}{7}x-1=-x\left(5x-\frac{10}{7}\right)-1\)
\(A\text{ có GTLN khi }-x\left(5x-\frac{10}{7}\right)\text{ có GTLN}\)
\(\text{Mà }-x\left(5x-\frac{10}{7}\right)\le0\)Dấu " = " xảy ra khi \(-x\left(5x-\frac{10}{7}\right)=0\text{ }\Rightarrow\orbr{\begin{cases}-x=0\\5x-\frac{10}{7}=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\5x=\frac{10}{7}\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{2}{7}\end{cases}}\)
\(\Rightarrow\text{ }Max\text{ }A=0-1=-1\text{ khi }x\in\left\{0\text{ ; }\frac{2}{7}\right\}\)
Bài giải
\(A=-5x^2+\frac{10}{7}x-1=-x\left(5x-\frac{10}{7}\right)-1\)
\(A\text{ đạt GTLN khi }-x\left(5x-\frac{10}{7}\right)\text{ đạt GTLN}\)
\(\text{Mà }-x\left(5x-\frac{10}{7}\right)\le0\) Dấu " = " xảy ra khi \(-x\left(5x-\frac{10}{7}\right)=0\text{ }\Rightarrow\orbr{\begin{cases}-x=0\\5x-\frac{10}{7}=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\5x=\frac{10}{7}\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{2}{7}\end{cases}}\)
\(\Rightarrow\text{ }Max\text{ }A=0-1=-1\text{ khi }x\in\left\{0\text{ ; }\frac{2}{7}\right\}\)