Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Với giá trị nào của x thì B = |x − 1| + |x − 2| + |x − 3| + |x − 5| đạt giá trị nhỏ nhất?
Với mọi x ta có: |x| ≥ x; dấu “=” xảy ra khi x ≥ 0. Do đó:
B = |x − 1| + |x − 2| + |3 − x| + |5 − x|
⇒ B ≥ x – 1 + x – 2 + 3 – x + 5 – x = 5
Dấu ''='' xảy ra khi và chỉ khi
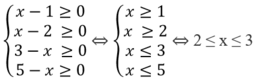
Vậy với 2 ≤ x ≤ 3 thì B đạt giá trị nhỏ nhất là 5.
Theo BDDT trị tuyệt đối\(B=\left|x-1\right|+\left|x-2\right|+\left|x-3\right|+\left|x-5\right|=\left(\left|x-1\right|+\left|5-x\right|\right)+\left(\left|x-2\right|+\left|3-x\right|\right)\)\(\ge\left|x-1+5-x\right|+\left|x-2+3-x\right|=5\)
=> Min B=5
Dấu bằng xảy ra khi \(\hept{\begin{cases}\left(x-2\right)\left(3-x\right)\ge0\\\left(x-1\right)\left(5-x\right)\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}2\le x\le3\\1\le x\le5\end{cases}\Leftrightarrow}2\le x\le3}\)
Ta có :
\(B=|x-1|+|x-2|+|3-x|+|5-x|\)
\(\Rightarrow B\ge x-1+x-2+3-x+5-x=5\)
Dấu ''='' xảy ra khi và chỉ khi
\(x-1\ge0\Leftrightarrow x\ge1\)
\(x-2\ge0\Leftrightarrow x\ge2\)\(3-x\ge0\Leftrightarrow x\le3\)
\(5-x\ge0\Leftrightarrow x\le5\)\(\Leftrightarrow2\le x\le3\)
Vậy với 2 ≤ x ≤ 3 thì B đạt giá trị nhỏ nhất là 5.
Ta có:
|x – 3| + |x – 7| = |x – 3| + |7 – x| ≥ |x – 3 + 7 – x| = |4| = 4.
(áp dụng bài 140: |x| + |y| ≥|x + y|)
* Lại có: |x – 5| ≥ 0.
Vậy A = |x – 3| + |x – 5| + |x – 7| ≥ 4 + 0 = 4.
Dấu ''='' xảy ra khi và chỉ khi: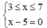 
, tức là x = 5.
Vậy với x = 5 thì A đạt giá trị nhỏ nhất là 4.
Ta biết rằng :\(|A|\ge A\)( Dấu "=" xảy ra khi và chỉ khi A \(\ge\) 0)
\(|A|=|-A|\) và \(|A|\ge0\)(Dấu ''='' xảy ra khi và chỉ khi A = 0)
Ta có: \(A=|x-3|+|x-5|+|x-7|\ge x-3+0+7-x=4\)
Dấu ''='' xảy ra khi và chỉ khi
\(\hept{\begin{cases}x-3\ge0\\x-5=0\\7-x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge3\\x=5\Leftrightarrow x=5\\x\le7\end{cases}}}\)
Vậy với x = 5 thì A đạt giá trị nhỏ nhất là 4.
\(P=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
\(P=\left[\left(x-1\right)\left(x+6\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]\)
\(P=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(P=\left(x^2+5x\right)^2\ge-36\)
\(\Rightarrow GTNN\) của \(P=-36\)
Dấu = sảy ra khi:\(x^2+5x=0\)
.....................\(\Rightarrow x=0\) hoặc \(x=-5\)
Chào Kirito
Đề ra:
Với giá trị nào của x thì B=|x−1|+|x−2|+|x−3|+|x−5| đạt giá trị nhỏ nhất?
Theo mình là nên dùng phương pháp xét dấu nhưng ko biết là bạn đã được học chưa :)
Nếu rồi thì bạn nhắn tin lại với mình mình giúp bạn :) còn chưa thì để mình nghĩ cách khác
Chứ xét dấu làm đơn giản nhưng hơi dài nên mình nghĩ mình nên hỏi bạn trước rồi mới làm
Chúc bạn một ngày vui vẻ
Ukm cậu dùng phương pháp đó cx được