Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn cần viết đề bằng công thức toán ( biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

a) Với m=1, ta có:
\(\left(1x+1\right)\left(x-1\right)-1\left(x-2\right)^2=5\)
\(\Leftrightarrow\)\(\left(x+1\right)\left(x-1\right)-\left(x-2\right)^2=5\)
\(\Leftrightarrow\)\(x^2-1-\left(x^2-2x+1\right)=5\)
\(\Leftrightarrow\)\(x^2-1-x^2+2x-1=5\)
\(\Leftrightarrow\)\(2x-2=5\)
\(\Leftrightarrow\)\(2x=7\)
\(\Leftrightarrow\)\(x=\frac{7}{2}\)
b) Để phương trình có nghiệm x=-3 hay phương trình nhận -3 làm nghiệm
ta có: \(\left(-3m+1\right)\left(-3-1\right)-m\left(-3-2\right)^2=5\)
\(\Leftrightarrow-4\left(-3m+1\right)-m\left(-5\right)^2=5\)
\(\Leftrightarrow12m-4-25m=5\)
\(\Leftrightarrow12m-25m=5+4\)
\(\Leftrightarrow-13m=9\)
\(\Leftrightarrow m=\frac{-9}{13}\)

a) Để phương trình trên là phương trình bậc nhất thì: m≠\(\dfrac{3}{8}\)
c) Để phương trình vô nghiệm thì: m=0
d) Để phương trình vô số nghiệm thì m=\(\dfrac{3}{8}\)
a/ \(\left(2m-3\right)x+\left(x-3\right)4m+2mx=0\)
\(\Leftrightarrow\left(8m-3\right)x-12m=0\)
Để phương trình là hàm số bậc 1 :
\(8m-3\ne0\Leftrightarrow m\ne\dfrac{3}{8}\)
b/ Phương trình vô nghiệm :
\(\Leftrightarrow\left\{{}\begin{matrix}8m-3=0\\12m\ne0\end{matrix}\right.\)
c/ Phương trình vô số nghiệm khi :
\(\Leftrightarrow\left\{{}\begin{matrix}8m-3=0\\12m=0\end{matrix}\right.\)

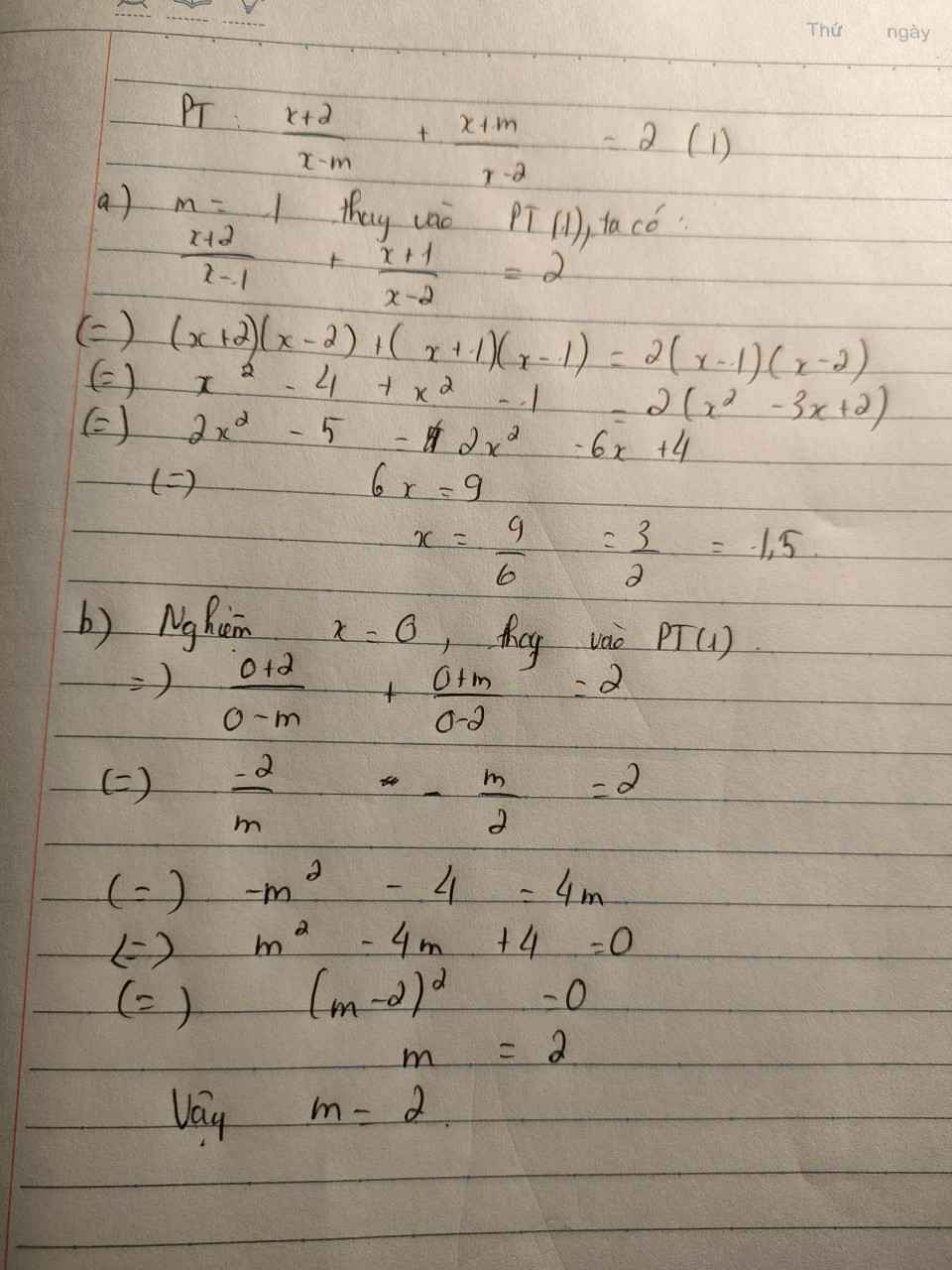
m = 1