Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Đường thẳng d đi qua điểm A( 1 ; 1 ;1); có một vecto chỉ phương là ( 2; -1; -1)
Mặt phẳng (P) có vecto pháp tuyến là
Ta có: u → . n → = 2.1 + (-1).1 + (-1).1 = 0 và A ∈ (P)
Suy ra, đường thẳng d thuộc mặt phẳng (P).

a)\(\Rightarrow d:4x+5y+14=0\)
\(d':4x+5y+14=0\)
Ta có: \(\dfrac{4}{4}=\dfrac{5}{5}=\dfrac{14}{14}\) \(\Rightarrow d\equiv d'\)
b) \(\Rightarrow d:x+2y-5=0\)
Ta có: \(\dfrac{1}{2}=\dfrac{2}{4}=\dfrac{-5}{-10}\) \(\Rightarrow d\equiv d'\)
c) Ta có: \(\dfrac{1}{2}\ne\dfrac{1}{1}\) \(\Rightarrow d\) cắt \(d'\)

Đáp án B
Đường thẳng d đi qua A(1 ; 2 ; 0); có vecto chỉ phương là u d → (5; 7; 6)
Mặt phẳng (P) có vecto pháp tuyến n p → (1; 1; 1)
Ta có: u d → . n p → = 5.1 + 7.1 + 6.1 = 18
Suy ra: đường thẳng d cắt mặt phẳng (P).

Đáp án A
*Gọi (Q) là mặt phẳng chứa d và vuông góc với mặt phẳng (Oxy). Để khoảng cách giữa hai đường thẳng d và ∆ nhỏ nhất thì ∆ chính là giao tuyến của hai mặt phẳng (Oxy) và mp (Q).
* Mặt phẳng (Oxy) có phương trình là z = 0 có VTPT n Oxy → = (0; 0; 1).
Đường thẳng d đi qua A(1;2; -3) và có VTCP u d → = (1; -2; 0)
Suy ra, VTPT của (Q) là n Q → = [ u d → ; n Oxy → ] = (2; 1; 0)
Phương trình mặt phẳng (Q) là: 2(x - 1) + 1(y - 2) + 0(z + 3) = 0
Hay 2x + y -4 =0
* Đường thẳng ∆ cần tìm là giao tuyến của hai mặt phẳng (Oxy) và (Q). Tập hợp các điểm thuộc ∆ là nghiệm hệ phương trình: 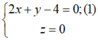
* Đặt x = 1 + t thay vào (1) ta được: y = 4 - 2x = 4 - 2(1 + t) = 2 - 2t
Suy ra, phương trình tham số của đường thẳng ∆ là: 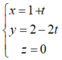

Đáp án B
Đường thẳng d 1 đi qua điểm M 1 (2; 0; -1) và có vectơ chỉ phương là u 1 → = (4; -6; -8);
đường thẳng d 2 đi qua điểm M 2 (7; 2; 0) và có vectơ chỉ phương là u 2 → = (-6; 9; 12).
Do hai vectơ u 1 → và u 2 → cùng phương nên các đáp án A và C là sai.
Thay tọa độ điểm M 1 vào d 2 , ta thấy:
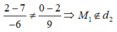
Do đó hai đường thẳng d 1 và d 2 song song.
Vậy đáp án B là đúng.
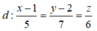


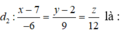
Đáp án C
Đường thẳng d đi qua điểm M(2 ;3 ;0) và có vectơ chỉ phương là u d → = (4; 1; -5), mặt phẳng (P) có vectơ pháp tuyến là u p → = (1; 1; 1). Ta có:
Suy ra đường thẳng d song song với mặt phẳng (P).