PA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PA
3
9 tháng 4 2022
triệt tiêu căn x dưới mẫu thì còn căn x trên tử thôi
HN
5 tháng 4 2022
\(\dfrac{-2m+1}{2}=1-2m\) \(\Leftrightarrow\) m=\(\dfrac{1}{2}\).
\(\dfrac{m-1}{2}=m-1\) \(\Leftrightarrow\) m=1.
Hai phương trình đã cho không là hai phương trình tương đương.
PA
1
27 tháng 2 2022
-Đặt \(\sqrt{x}=a\Rightarrow x=a^2\)
\(x+\sqrt{x}-6=a^2+a-6=a^2-2a+3a-6=a\left(a-2\right)+3\left(a-2\right)=\left(a-2\right)\left(a+3\right)=\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)\)
2 tháng 3 2022
\(x^2+x^2-14x+49=169\)
\(\Leftrightarrow2x^2-14x-120=0\)
\(\Leftrightarrow2\left(x^2-7x-60\right)=0\)
\(\Leftrightarrow x^2-7x-60=0\)
Đó bạn
19 tháng 8 2021
Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
19 tháng 8 2021
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2
25 tháng 10 2021
\(\sqrt{0,81.a^{10}\left(x^2-2x+1\right)}=\sqrt{\left(0,9\right)^2.\left(a^5\right)^2\left(x-1\right)^2}\)
\(=0,9.\left|a^5\left(x-1\right)\right|=0,9.\left|a^5x-a^5\right|\)
TD
6 tháng 2 2022
=\(\left(\dfrac{2\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}}{\sqrt{x}+3}\right).\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
=\(\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)+\sqrt{x}\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{\left(x-9\right)\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
=\(\dfrac{2x+6\sqrt{x}+\sqrt{x}\left(x-\sqrt{x}-6\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}.\dfrac{1}{\sqrt{x}}\)
=\(\dfrac{2x+6\sqrt{x}+x\sqrt{x}-x-6\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{x+x\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{x+\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}\)
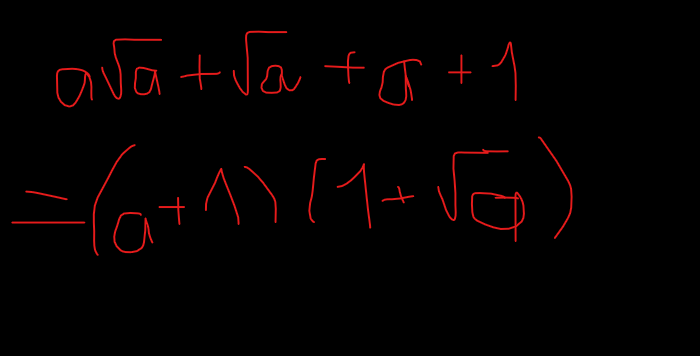
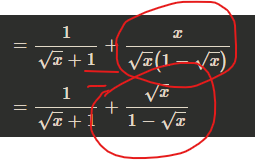
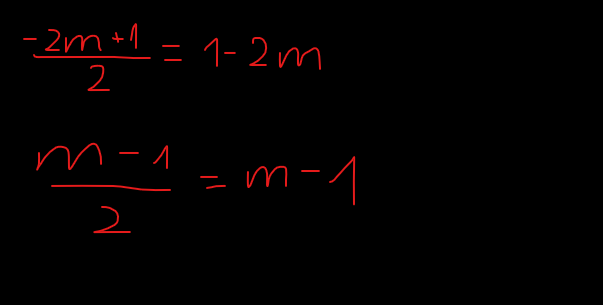
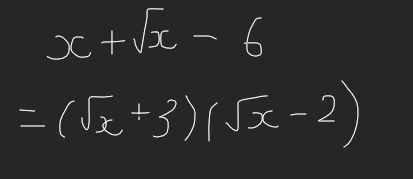
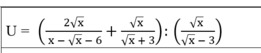
\(a\sqrt{a}+\sqrt{a}+a+1\)
\(=\sqrt{a}\left(a+1\right)+\left(a+1\right)\)
\(=\left(a+1\right)\left(\sqrt{a}+1\right)=\left(a+1\right)\left(1+\sqrt{a}\right)\)
Đặt \(\sqrt{a}\) ra đó bạn