Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có thể kết luận được tam giác ABC bằng tam giác A’B’C’ (trường hợp c.g.c)

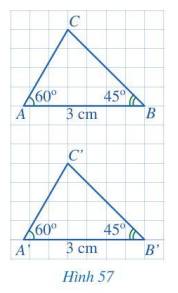
Hai tam giác trên có :
∠A = ∠A' ; ∠B = ∠B' ; ∠C = ∠C'
Nhận xét: Hai tam giác trên bằng nhau

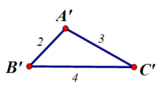
BC = B’C’ = 6 (ô vuông).
Tam giác ABC và A’B’C’ có các cặp cạnh tương ứng bằng nhau nên tam giác ABC bằng tam giác A’B’C’ (c.c.c)

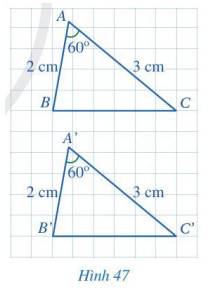
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)

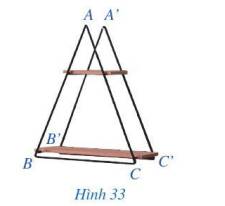
Tam giác ABC có bằng tam giác A’B’C’ (vì 2 tam giác này có thể chồng khít lên nhau).

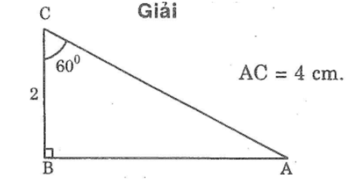
+ Vẽ tam giác ABC:
-) Vẽ đoạn thẳng BC = 2 cm.
-) Trên cùng một nửa mặt phăng bờ BC, vẽ các tia Bx và Cy sao cho ∠CBx = 90º và &BCy = 60º.
Hai tia trên cắt nhau tại A ta được tam giác ABC.
+) Đo AC ta được: AC = 4cm.

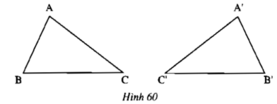
a) AB = A’B’; BC = B’C’; CA = C’A’.
A = A’; B = B’; C = C’.
b) Hai tam giác ABC và A’B’C’ có bằng nhau vì chúng có các cặp cạnh và cặp góc tương ứng bằng nhau.
c) Hai hình tam giác ABC và A’B’C’ có thể đặt chồng khít lên nhau.
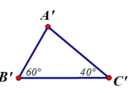
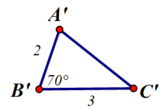
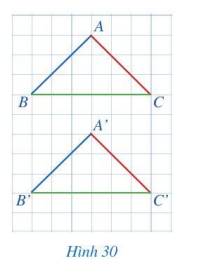
ΔABC và ΔA’B’C’ có:
AB = A’B’
∠B = ∠B'
BC = B’C’
⇒ ΔABC = ΔA’B’C’ (cạnh – góc – cạnh)