K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 1 2022
a: Xét tứ giác BFCE có
D là trung điểm của BC
D là trung điểm của FE
Do dó: BFCE là hình bình hành
b: Xét tứ giác ABFE có
AB//FE
AB=FE
Do đó: ABFE là hình bình hành
mà \(\widehat{FAB}=90^0\)
nên ABFE là hình chữ nhật
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2023
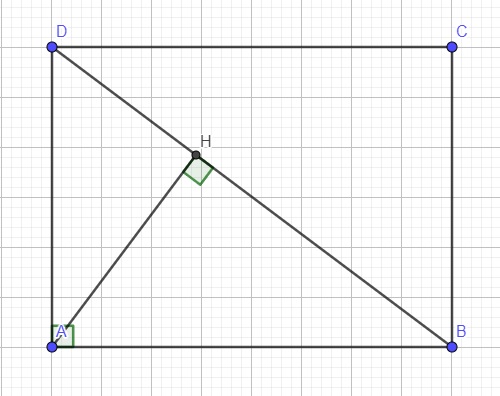
a.
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)
21 tháng 10 2021
Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
hay MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành
31 tháng 3 2022
a: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
góc B chung
Do đó: ΔAHB\(\sim\)ΔCAB
Suy ra: BA/BC=BH/BA
hay \(BA^2=BH\cdot BC\)
b: \(AC=\sqrt{BC^2-AB^2}=24\left(cm\right)\)
\(HC=\dfrac{AC^2}{BC}=\dfrac{24^2}{40}=14.4\left(cm\right)\)
8 tháng 4 2022
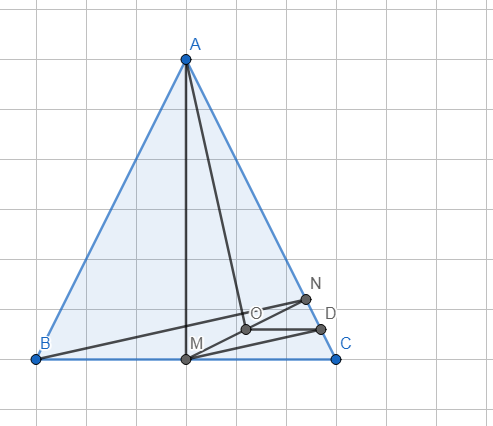
c) -Gọi D là t/đ CN.
-△BCN có: MD là đg trung bình (M t/đ BC, D t/đ CN)
\(\Rightarrow\)MD//BN
-△MNC có: OD là đg trung bình (O t/đ MN, D t/đ CN)
\(\Rightarrow\)OD//MC \(\Rightarrow\)OD⊥AM.
-△AMD có: MN là đg cao, DO là đg cao, MN cắt DO tại O.
\(\Rightarrow\)O là trực tâm △AMD \(\Rightarrow\)AO⊥MD \(\Rightarrow\)AO⊥BN
8 tháng 9 2021
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED
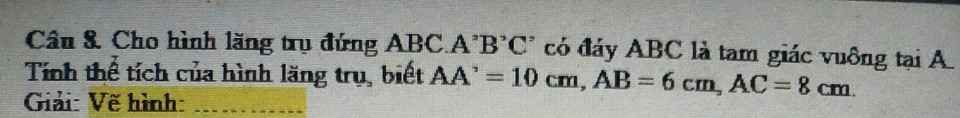
có : \(AH\perp BD\)
\(CK\perp DB\) =>AH//CK
Có : tứ giác ABCD là hình bình hành :
`=>` AB//CB
`=> góc ADB = góc gocd DBC
Xét tam giác `ADH` và tam giác `CBK` có
`AB = CB`(tứ giác ABCD là hbh)
`AHD = CKB = 90^0`
`ADH = CBK(c/mt)`
`=> tam giác ADH = tam giác BCK(ch-gn)
`=> AH = CK`(t/ứng)
xét tg BHCK có :
`AH = Ck`
`AH//CK`
`=> tg BHCK là hình bình hành