Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
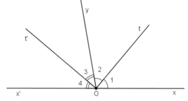
Vì \(x\widehat{O}y\) và \(y\widehat{O}x'\) là 2 góc kề bù
\(\Rightarrow x\widehat{O}y+y\widehat{O}x'=180^o\)
\(130^o+y\widehat{O}x'=180^o\)
\(y\widehat{O}x'=180^o-130^o\)
\(y\widehat{O}x'=50^o\)
Vì Ot là tia p/g của \(x\widehat{O}y\)
\(\Rightarrow x\widehat{O}t=t\widehat{O}y=\dfrac{x\widehat{O}y}{2}=\dfrac{130^o}{2}=65^o\)
\(\Rightarrow t\widehat{O}y+y\widehat{O}x'=t\widehat{O}x'\)
\(65^o+50^o=t\widehat{O}x'\)
⇒\(t\widehat{O}x'=115^o\)
Chúc bạn học tốt!

góc x'Oy = 180 - 100 = 80o
góc yOt' = 80 : 2 = 40o
góc tOy = 100 : 2 = 50o
góc x'Ot = 80 + 50 = 130o
góc xOt' = 100 + 40 = 140o
góc tOt' = 50 + 40 = 90o

bạn tự vẽ hình nha
Giải
Có xOy và yOx' là 2 góc kề bù
=> xOy+yOx'=180 độ
Thay số : 100 độ+ yOx'=180 độ
=> yOx'=80 độ
Có tia Ot là phân giác của xOy
=>xOt=tOy=100 độ / 2= 50 độ
Có tia Ot' là phân giác của x'Oy
=>x'Ot'=t'Oy=80 độ / 2 = 40 độ
Có xOt' và x'Ot' là 2 góc kề bù
=> xOt'+x'Ot'=180 độ
Thay số: xOt'+40 độ = 180 độ
=> xOt'=140 độ
Có xOt và x'Ot là 2 góc kề bù
=>xOt+x'Ot=180 độ
Thay số: 50 độ+x'Ot=180 độ
=>x'Ot=130 độ
Trên cùng một nửa mặt phẳng bờ chứa tia Ox có xOt Tia Ot nằm giữa tia Ox và tia Ot'
=>xOt+tOt'=xOt'
thay số: 50 độ+tOt'=140 độ
=>tOt'=90 độ

Ta có: tia Ot là tia phân giác của \(\widehat{xOy}\)
nên \(\widehat{xOt}=\dfrac{\widehat{xOy}}{2}=\dfrac{100^0}{2}=50^0\)
Ta có: \(\widehat{xOt}+\widehat{x'Ot}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{x'Ot}+50^0=180^0\)
hay \(\widehat{x'Ot}=130^0\)
Vậy: \(\widehat{x'Ot}=130^0\)
Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{x'Oy}+100^0=180^0\)
hay \(\widehat{x'Oy}=80^0\)
Ta có: tia Ot' là tia phân giác của \(\widehat{x'Oy}\)
nên \(\widehat{x'Ot'}=\dfrac{\widehat{x'Oy}}{2}=\dfrac{80^0}{2}=40^0\)
Ta có: \(\widehat{xOt'}+\widehat{x'Ot'}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{xOt'}+40^0=180^0\)
hay \(\widehat{xOt'}=140^0\)
Vậy: \(\widehat{xOt'}=140^0\)

Làm trước , vẽ hình sau
Vì Ot là tia phân giác của góc xOy
\(\Rightarrow\)góc xOt=góc tOy = \(\dfrac{100độ}{2}\)= 50 độ
Ta có : góc x'Oy + góc yOt = góc x'Ot ( hai góc kề nhau )
... Tự thay vào tính nhá
Tương tự , tính góc xOt'
Còn góc tOt' thì
tOt' = \(\dfrac{xOy}{2}+\dfrac{x'Oy}{2}\)( Vì phân giác đó )
tOt' = \(\dfrac{xOy+yOx'}{2}\)= \(\dfrac{180}{2}\)= 90 độ

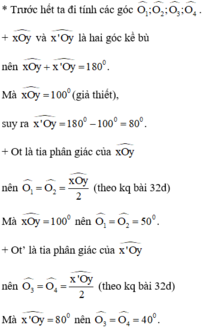
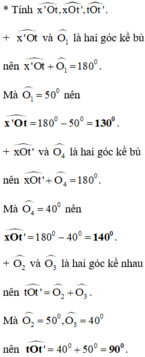
Giải:
Vì \(x\widehat{O}y\) và \(y\widehat{O}x'\) là 2 góc kề bù
\(\Rightarrow x\widehat{O}y+y\widehat{O}x'=180^o\)
\(70^o+y\widehat{O}x'=180^o\)
\(y\widehat{O}x'=180^o-70^o\)
\(y\widehat{O}x'=110^o\)
Vì Ot là tia p/g của \(x\widehat{O}y\)
\(\Rightarrow x\widehat{O}t=t\widehat{O}y=\dfrac{x\widehat{O}y}{2}=\dfrac{70^o}{2}=35^o\)
Vì Ot' là tia p/g của \(y\widehat{O}x'\)
\(\Rightarrow y\widehat{O}t'=t'\widehat{O}x'=\dfrac{y\widehat{O}x'}{2}=\dfrac{110^o}{2}=55^o\)
\(\Rightarrow t\widehat{O}y+y\widehat{O}t'=t\widehat{O}t'\)
\(35^o+55^o=t\widehat{O}t'\)
\(\Rightarrow t\widehat{O}t'=90^o\)
\(\Rightarrow x\widehat{O}y+y\widehat{O}t'=x\widehat{O}t'\)
\(70^o+55^o=x\widehat{O}t'\)
\(\Rightarrow x\widehat{O}t'=125^o\)
Chúc bạn học tốt!