Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 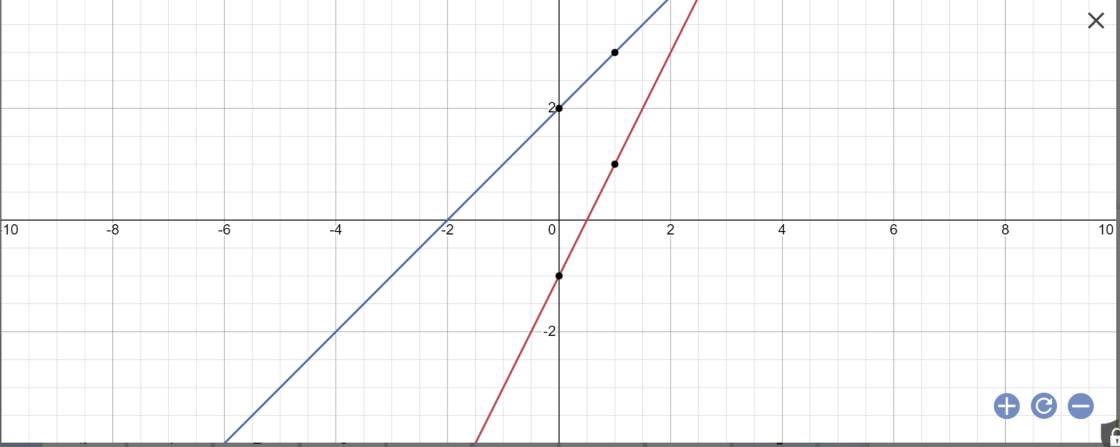
b: Phương trình hoành độ giao điểm là:
2x-1=x+2
=>x=3
Thay x=3 vào y=x+2, ta được:
y=3+2=5
c: Vì (d)//(d1) nên (d): y=2x+b
Thay x=1 và y=0 vào (d), ta được:
b+2=0
=>b=-2
=>y=2x-2

a: 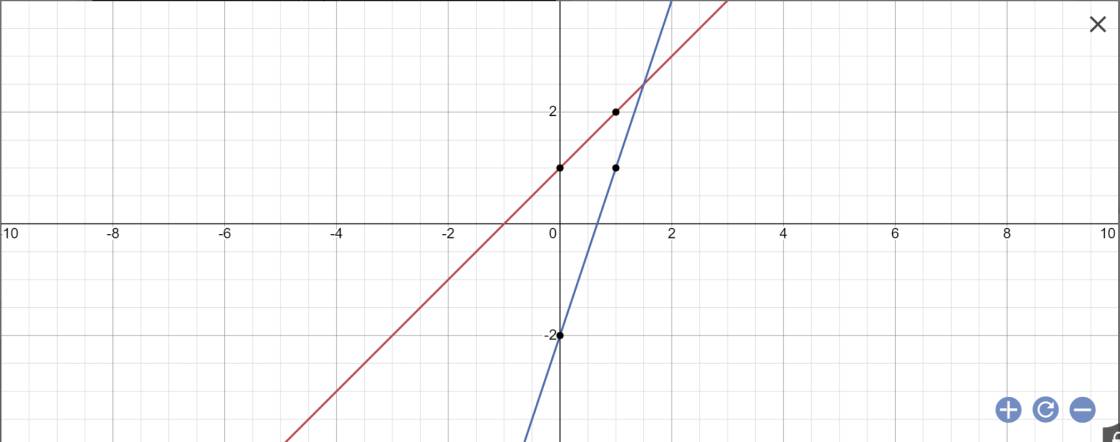
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-2=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-x=2+1\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=3\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{3}{2}+1=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=3/2 và y=5/2 vào (d3), ta được:
\(2m+3\cdot\dfrac{3}{2}-1=\dfrac{5}{2}\)
=>\(2m+\dfrac{7}{2}=\dfrac{5}{2}\)
=>\(2m=-1\)
=>m=-1/2
c: (d3): y=2m+3x-1
=>y=m*2+3x-1
Tọa độ điểm mà (d3) luôn đi qua là:
\(\left\{{}\begin{matrix}2=0\left(vôlý\right)\\y=3x-1\end{matrix}\right.\)
=>(d3) không đi qua cố định bất cứ điểm nào

Tọa độ giao điểm của (d2) và (d3) là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}x+1=-x+3\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Thay x=1 và y=2 vào (d1), ta được:
\(\left(m^2-1\right)+m^2-5=2\)
=>\(2m^2=8\)
=>\(m^2=4\)
=>\(\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\)

b: Để hai đường thẳng cắt nhau tại một điểm trên trục tung thì m-1=15
hay m=16

Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}mx+2y=m+1\\2x+my=2m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2mx+4y=2m+2\\2mx+m^2y=2m^2-m\end{matrix}\right.0\Leftrightarrow\left\{{}\begin{matrix}2mx+m^2y-2mx-4y=2m^2-m-2m-2\\mx+2y=m+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y\left(m^2-4\right)=2m^2-3m-2\\mx+2y=m+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y\left(m-2\right)\left(m+2\right)=\left(m-2\right)\left(2m+1\right)\\mx+2y=m+1\end{matrix}\right.\)(1)
TH1: m=2
Hệ phương trình (1) sẽ trở thành:
\(\left\{{}\begin{matrix}y\left(2-2\right)\left(2+2\right)=\left(2-2\right)\left(2\cdot2+1\right)\\2x+2y=2+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}0y=0\\2x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y\in R\\2x+2y=3\end{matrix}\right.\)
Vậy: Khi m=2 thì (d1) và (d2) trùng nhau
TH2: m=-2
Hệ phương trình (1) sẽ trở thành:
\(\left\{{}\begin{matrix}y\cdot\left(-2-2\right)\left(-2+2\right)=\left(-2-2\right)\left(-2\cdot2+1\right)\\-2x+2y=-2+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}0y=\left(-4\right)\cdot\left(-3\right)=12\\-2x+2y=-1\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)
Vậy: Khi m=-2 thì (d1)//(d2)
TH3: \(m\notin\left\{2;-2\right\}\)
hệ phương trình (1) sẽ trở thành:
\(\left\{{}\begin{matrix}y=\dfrac{\left(m-2\right)\left(2m+1\right)}{\left(m-2\right)\left(m+2\right)}=\dfrac{2m+1}{m+2}\\mx+2y=m+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{2m+1}{m+2}\\mx=m+1-\dfrac{4m+2}{m+2}=\dfrac{\left(m+1\right)\left(m+2\right)-4m-2}{m+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{2m+1}{m+2}\\x=\dfrac{m^2+3m+2-4m-2}{m\left(m+2\right)}=\dfrac{m^2-m}{m\left(m+2\right)}=\dfrac{m-1}{m+2}\end{matrix}\right.\)
vậy: Khi \(m\notin\left\{2;-2\right\}\) thì (d1) cắt (d2) tại \(A\left(\dfrac{m-1}{m+2};\dfrac{2m+1}{m+2}\right)\)

a) Vẽ tương đối (d1), (d2)
b) Phương trình hoành độ giao điểm của (d1) và (d2):
\(\frac{3}{2}\)\(x+6\)\(=\) \(-3x-3\)
\(\Leftrightarrow\)\(\frac{9}{2}\)\(x=\)\(-9\)
\(\Leftrightarrow\)\(x=\)\(-2\)
\(\Rightarrow\)\(y=3\)
Vậy giao điểm của (d1) và (d2) là \(\left(-2;3\right)\)
c) Gọi phương trình đường thẳng cần tìm là (d): y = ax + b
(d) // (d1) => (d):\(\frac{3}{2}\) \(x+b\)
A \(\in\)(d2) => A \((\)\(\frac{-4}{3}\)\(;1\)\()\)
Thay tọa độ A vào đường thẳng (d) ta có :
1 = \(\frac{3}{2}\) .\(\frac{-4}{3}\)+ b
\(\Leftrightarrow\)b = 3
Vậy (d): y =\(\frac{3}{2}\) \(x+3\)
:3


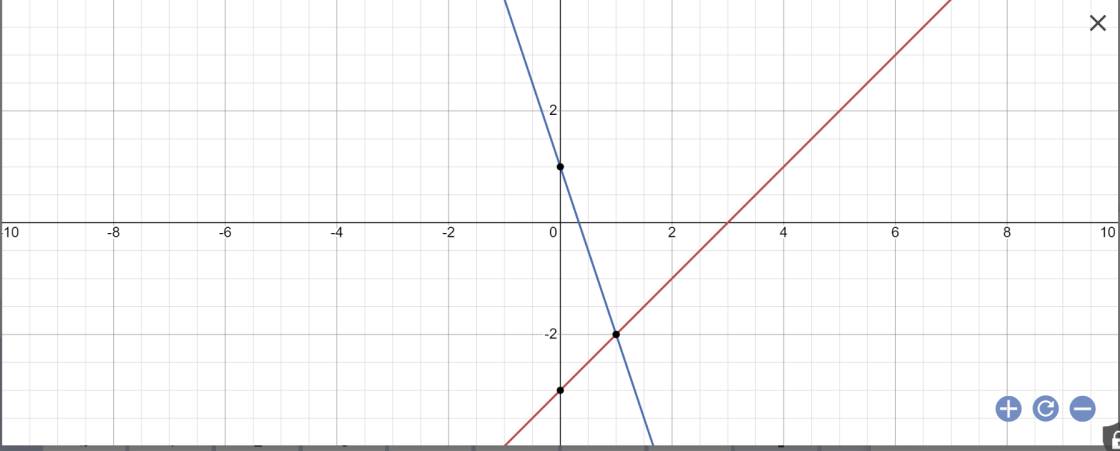
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+y=2\\2x+3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=-4\end{matrix}\right.\)
Thay x=6 và y=-4 vào (d3), ta được:
\(3\cdot6+2\cdot\left(-4\right)=10\left(đúng\right)\)
Vậy: (d3) đi qua giao điểm của (D1) và (D2)