Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{12}=\dfrac{1}{36}+\dfrac{1}{d'}\Rightarrow d'=18cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{36}{18}\Rightarrow h'=0,5cm\)

Đây là thấu kính hội tụ.
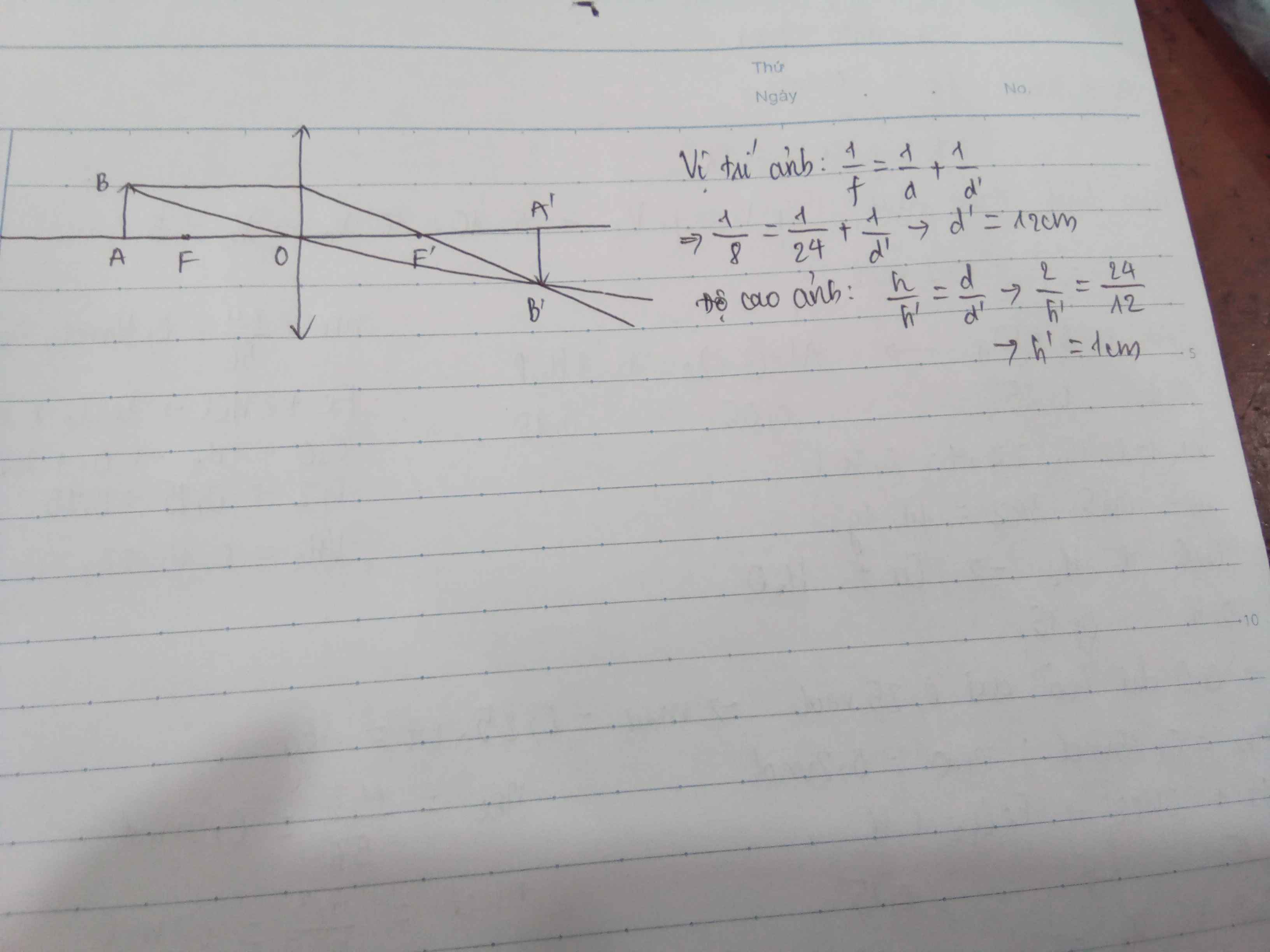
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{8}\Rightarrow d'=4,8cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{8}{4,8}\Rightarrow h'=0,6cm\)

Ảnh thật, ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{9}+\dfrac{1}{d'}\)
\(\Rightarrow d'=18cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{9}{18}\Rightarrow h'=2cm\)

b) ΔABF ~ ΔOIF
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{1}{A'B'}=\dfrac{54-18}{18}\)
=> A'B' = 0,5cm
ΔABO ~ ΔA'B'O
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{AO}{A'O}\Rightarrow A'O=\dfrac{A'B'.AO}{AB}=\dfrac{0,5.54}{1}=27cm\)

b)
b)
Tóm tắt:
OF = OF' = f = 12cm
OA = d = 18cm
AB = h = 10cm
A'B' = ?
OA' = ?
Giải:
\(\Delta ABF\sim\Delta OIF\)
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{10}{A'B'}=\dfrac{18-12}{12}\)
\(\Rightarrow A'B'=\dfrac{10.12}{18-12}=20cm\)
\(\Delta OAB\sim\Delta OA'B'\)
\(\Rightarrow\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\Leftrightarrow\dfrac{18}{OA'}=\dfrac{10}{20}\Rightarrow OA'=\dfrac{18.20}{10}=36cm\)