Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 : Bài giải
Ta có : \(\widehat{A}-\widehat{B}=10^o\text{ }\Rightarrow\text{ }\widehat{A}=\widehat{B}+10^o\)
Trong tứ giác ABCD có :
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{B}+10+\widehat{B}+60^o+80^o=360^o\)
\(2\widehat{B}+150^o=360^o\)
\(2\widehat{B}=110^o\)
\(\widehat{B}=55^o\text{ }\Rightarrow\text{ }\widehat{A}=65^o\)

Ta có tổng 4 góc trong tứ giác là: \(360^o\)
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
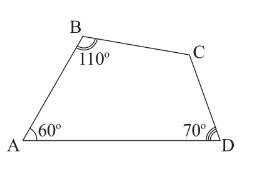
Hay: \(60^o+110^o+\widehat{C}+70^o=360^o\)
\(\Rightarrow\widehat{C}=360^o-\left(110^o+60^o+70^o\right)120^o\)
Vậy chọn đáp án A

bài 5; tính số đo các góc của tứ giác ABCD biết góc A = 60 độ; góc B = 90 độ. Tính số đo của góc C và góc D:
a, góc C = 100 độ; góc D = 60 độ;
góc A
C, góc B = 80 độ; góc C = 60 độ; 5 góc A = 6 góc D

Tổng bốn góc của 1 tứ giác bằng 360 ° nên: ∠A + ∠ B + ∠ C + ∠ D = 360 °
Suy ra: ∠ A + ∠ B = 360 ° – ( ∠ C + ∠ D) hay
∠ A + ∠ B = 360 ° - 60 ° + 80 ° = 220 °
Mà ∠ A - ∠ B = 10 °
Vậy
∠
A = 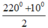 =
115
°
,
∠
B =
115
°
-
10
°
=
105
°
=
115
°
,
∠
B =
115
°
-
10
°
=
105
°

\(a,=>\angle\left(B\right)+\angle\left(C\right)=100+80=180^o\)
mà 2 góc ở vị trí trong cùng phía \(=>AB//CD\)
=>ABCD là hình thang
b,\(\dfrac{\angle\left(A\right)}{\angle\left(D\right)}=\dfrac{6}{4}=>\angle\left(A\right)=\dfrac{6\angle\left(D\right)}{4}\)
\(=>\angle\left(A\right)+\angle\left(D\right)=180^o\)(góc trong cùng phía)
\(=>\dfrac{6\angle\left(D\right)}{4}+\angle\left(D\right)=180^o=>\angle\left(D\right)=72^o=>\angle\left(A\right)=\dfrac{6.72^0}{4}=108^o\)

Lời giải:
Ta có: $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0$ (tổng 4 góc trong 1 tứ giác)
$\Rightarrow \widehat{D}=360^0-(\widehat{A}+\widehat{B}+\widehat{C})$
$=360^0-(75^0+115^0+100^0)=70^0$
Đáp án A.
Chọn B