Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
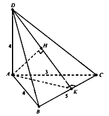
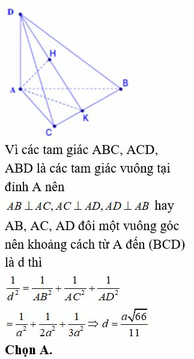
Vì B C 2 = B A 2 + A C 2 nên ∆ A B C vuông tại A.
Gọi K là hình chiếu của A lên BC, H là hình chiếu của A lên DK.
Ta có 1 A H 2 = 1 A D 2 + 1 A K 2 = 1 A D 2 + 1 A B 2 + 1 A C 2
= 1 4 2 + 1 4 2 + 1 3 2 = 17 72 ⇒ d A ; A B C D = A H = 72 17 = 12 34

Đáp án B
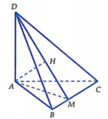
Ta có A B 2 + A C 2 = B C 2 ⇒ tam giác ABC vuông tại A.
Trong (ABC) kẻ AM vuông góc tại M ⇒ 1 A M 2 = 1 A B 2 + 1 A C 2
Trong (DAM) kẻ A H ⊥ D M tại H.
Ta có
D A ⊥ B C ; A M ⊥ B C ⇒ D A M ⊥ B C ⇒ D A M ⊥ D B C
D A M ⊥ D B C D A M ∩ D B C = D M A H ⊂ D A M ; A H ⊥ D M ⇒ A H ⊥ D B C
⇒ d A ; D B C = A H
Tam giác DAM vuông tại A có AH là đường cao
⇒ 1 A H 2 = 1 A M 2 + 1 A D 2 = 1 A B 2 + 1 A C 2 + 1 A D 2 = 1 3 2 + 1 4 2 + 1 4 2 = 17 72 ⇒ A H = 12 34

Chọn B
Gọi I là trung điểm AB, J là trung điểm CD
Từ AC=AD=BC=BD =>IJ chính là đoạn vuông góc chung của 2 đường thẳng AB và CD
=> IJ = a
Gọi O là điểm cách đều 4 đỉnh => O là tâm mặt cầu ngoại tiếp tứ diện ABCD
=> O nằm trên IJ => Ta cần tính OA
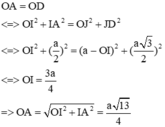
Ta có:

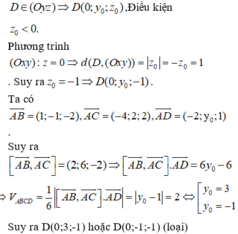
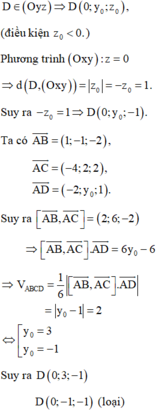


Đáp án C
Phương pháp giải:
Áp dụng công thức tính nhanh thể tích của tứ diện gần đều, đưa bài toán tính khoảng cách về bài toán tìm thể tích chia cho diện tích đáy (tính theo công thức Hê – rông)
Lời giải: