Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
x M = k λ D a ⇒ λ = a x M k D = 4 , 5 k μ m 0 , 38 ≤ λ = 4 , 5 k ≤ 0 , 76 ⇒ 5 , 9 ≤ k ≤ 11 , 8 ⇒ k = 6 ; 7 ; 8 ; 9 ; 10 ; 11
k = 6 ⇒ λ = 0 , 75 μ m ; k = 7 ⇒ λ = 9 14 μ m ; k = 8 ⇒ λ = 0 5625 μ m ; k = 9 ⇒ λ = 5 μ m ; k = 10 ⇒ λ = 0,45 μ m ; k = 11 ⇒ λ = 9 22 μ m ;

Ta có
7 i 1 = 7mm ⇒ i 1 = 1mm = λ 1 D/a ⇒ λ 1 = 0,5 μ m
7 i 1 = k i đ ⇒ 7 λ 1 = k λ đ ⇒ λ đ = 7 λ 1 /k μ m
Ta có một loại trị số của λ đ ứng với những trị số khác nhau của k
λ đ (μm): 3,5; 1,15; 1,17; 0,875; 0,7; 0,583; 0,5; 0,4375
chỉ có chỉ số λ đ = 0,7 là thích hợp.

Chọn đáp án A
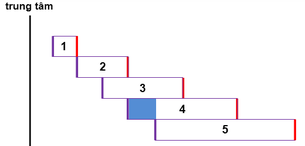
Ta biểu diễn quang phổ bậc 1, 2, 3, 4, 5 như trên hình.
Từ hình vẽ → phần chồng chất lên nhau giữa quang phổ bậc 3 và bậc 4 mà không chưa quang phổ bậc 5 là vùng tô xanh, ứng với khoảng từ bậc 4 đến bậc 5 của ánh sáng tím.
→ Δ L = x t 5 − x t 4 = 5 − 4 . 0 , 38.2 2 = 0 , 38 mm.

Ta có: \(x=k.\dfrac{\lambda D}{a}\)
\(\Rightarrow\lambda=\dfrac{ax}{kD}=\dfrac{0,4.5}{k.0,8}\mu m\)
Mà theo đề bài ta có:
\(0,38\mu m\le\lambda\le0,76\mu m\)
\(\Rightarrow\) Có 3 giá trị k thỏa mãn (k=4,5,6)

Bề rộng quang phổ bậc 2: ∆i2 = 2D(λt – λd)/a
→a = 2D(λt – λd)/ ∆i2 = 0,96 mm
Chọn đáp án B

Phương pháp:
Quang phổ ngay sát vạch sáng trung tâm là quang phổ bậc 1
Công thức tính bề rộng quang phổ bậc n : ∆xn = xđn - xtn
Cách giải:
Bề rộng quang phổ bậc 1 là:
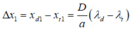
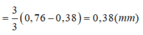
Đáp án A

Chọn A.
Khoảng vân ứng với ánh sáng đỏ là i i = 0 , 4 . 10 - 6 . 3 3 . 10 - 3 = 0 , 4 . 10 - 3 ( m ) = 0,40mm.
Bề rộng của quang phổ thứ nhất là d = 0,75mm – 0,40mm = 0,35mm.
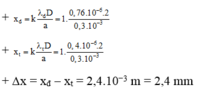

Đáp án D
+ Giả sử M là vị trí của vân sáng, khi đó ta có
+ Khoảng giá trị của bước sóng
0,38 μm ≤ λ ≤ 0,76 μm → có 5 giá trị của k thõa mãn
+ Nhập số liệu: Mode → 7
f ( x ) = 4 X , với X được gán bằng k
+ Xuất kết quả: =
· Start: giá trị đầu của X
· End: giá trị cuối của X
· Step: bước nhảy của X