Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Sử dụng công thức về vị trí vân sáng trong thí nghiệm giao thoa khe Yang
Cách giải: Vị trí vân sáng thỏa mãn điều kiện:
![]()
Do ở cùng 1 vị trí x mà có nhiều vân sáng thì ta có
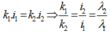
Mà ![]()
Thay số vào ta có:
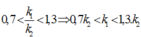
Ta sử dụng phương pháp thử các giá trị của k vào, vì k nguyên, ta lần lượt thay các giá trị k2 và tìm k1, sao cho k1 ≠ k2.
Ta có bảng:
| k2 |
Giá trị k1 |
k1 |
Giá trị tm |
| 1 |
0,7 < k1 <1,3 |
1 |
ktm |
| 2 |
1,4 < k1 < 2,6 |
2 |
ktm |
| 3 |
2,1 < k1 < 3,9 |
3 |
ktm |
| 4 |
2,8 < k1 < 5,2 |
3,4,5 |
3,5 |
| 5 |
3,5 < k1 < 6,5 |
4,5,6 |
4,6 |
Với k2 = 4; k1 = 3 thì λ2 = 435nm ; k1 = 5 thì λ2 = 725nm
Với k2 = 5; k1 = 4 thì λ2 = 464nm; k1 = 6 thì λ2 = 696nm
Vậy chon giá trị λ2 = 725nm.

Ta có:
\(k\lambda = k'\lambda'\Rightarrow \lambda'=\frac{580.k}{k'} \Rightarrow 415\leq \frac{580.k}{k'}\leq760\Rightarrow \frac{29.k}{38}\leq k' \leq \frac{116.k}{83}\)
Theo giả thiết, bất phương trình trên chỉ có thể có 3 nghiệm nguyên.
Lần lượt thế 4 giá trị của k vào => k = 5

![]()
Khoảng cách ngắn nhất giữa hai vân sáng cùng màu với vân trung tâm là
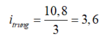
Dễ thấy 3,6 = 2.1,8 → Vị trí cùng màu vân trung tâm và gần vân trung tâm nhất ứng với vân sáng bậc 2 của λ1

Đáp án D

Chọn B
Ta có i1 = 1,8 mm ứng với λ = 0,6μm.
i12 = 3,6 mm => λ12 = 1,2μm.
Ở đây λ12 chỉ chia hết cho λ = 0,4μm.


Đáp án B
*Trên mà quan sát được 3 vân sáng tức là có 3 phổ chồng lên nhau
Khi đó phổ bậc k của bước sóng λ m i n sẽ trùng với phổ bậc k – 2 của bước sóng λ. Do đó ta có
k m i n = 5 Như vậy từ phổ bậc 3 trở đi có sự chồng lấn. Giả sử trong số 3 phổ chồng lấn gần O nhất là phổ bậc 3, bậc 4 và bậc 5 có một phổ bậc m (với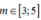 ) của màu vàng thuộc 1 trong 3 phổ đó thì khi đó ta có
) của màu vàng thuộc 1 trong 3 phổ đó thì khi đó ta có
=> Không tồn tại giá trị nguyên của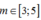
v Do đó ta tiếp tục xét sự chồng lấn của 3 quang phổ liền kề là phổ bậc 4, bậc 5 và bậc 6. Khi đó:
Như vậy có ba vân sáng tương ứng ba phổ chồng lên nhau trong đó có phổ bậc 5 của màu vàng.