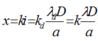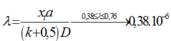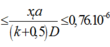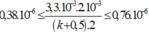Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D

*Khoảng có bề rộng nhỏ nhất mà không có vân sáng nào quan sát được trên màn tương ứng nằm ở dưới phía liền kề khi có hai quang phổ chồng lên nhau
*Bây giờ chúng ta đi xác định phổ bậc bao nhiêu thì có sự chồng lên nhau.
Áp dụng công thức tính k nhanh:
Do khoảng bề rộng nhỏ nhất nên có hai quang phổ chồng lên nhau suy ra n=1.
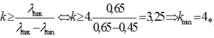
. Như vậy ở phổ bậc bắt đầu có 3 sự trùng nhau nên dưới phổ bậc 3 là có khoảng tối nhỏ nhất. QP bậc 3 có một phần chồng với quang phổ bậc 4. Do đó QP bậc 2 và 3 không chồng lên nhau. (Quan sát hình 1).
Do đó 
Phương pháp tổng quát.
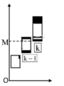
Ta lấy lấy vân sáng bậc k làm chuẩn. Từ đó chúng ta đi xác định k. Xác định được kmin tức là chúng ta đã biết được tại quang phổ bậc bao nhiêu bắt đầu có sự chồng lên nhau. Khi biết được từ quang phổ bậc bao nhiêu có sự chồng nhau thì bài toán trở nên vô cùng đơn giản.
Tại một vị trí có m quang phổ chồng lên nhau tức là có m vân sáng quan sát được
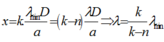
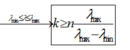
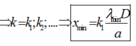

Màu sắc của vân trung tâm được tạo thành do sự chồng chập của ba ánh sáng đơn sắc λ 1 , λ 2 , λ 3
Vậy toạ độ những vân sáng cùng màu vân trung tâm thoả mãn
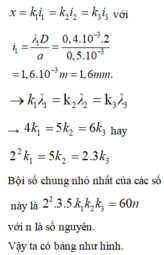

Vậy ta thấy giá trị khả dĩ lớn nhất của n bằng 4.
Vậy tổng số vân cùng màu vân trung tâm là N = 1 + 2.4 = 9 vân.
Đáp án C