Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Ta chú ý rằng có (n+1) vân sáng liên tiếp thì cách nhau d = n i
Suy ra, nếu ta xét d = i 123 = n x i x thì có n + 1 vân của bức xạ λ x khoảng ở giữa có n + 1 − 1 − 1 = n − 1 vân (vì không xét 2 vân ở mút)
+ Từ đó ta thiết lập:
i 123 = 12 i 1 = 9 i 2 = 8 i 3 = 3 i 12 = i 23 = 4 i 13
Giải thích lập tỷ số
i 1 i 2 = λ 1 λ 2 = 3 4 ⇒ i 12 = 4 i 1 = 3 i 2 ( 1 ) i 2 i 3 = λ 2 λ 3 = 8 9 ⇒ i 23 = 9 i 2 = 8 i 3 ( 2 ) i 3 i 1 = λ 3 λ 1 = 3 2 ⇒ i 31 = 2 i 3 = 3 i 1 ( 3 ) i 12 i 3 = 4 i 1 3 i 1 / 2 = 8 3 ⇒ i 123 = 3 i 12 = 8 i 3 ( 4 )
Từ (1); (2); (3) ta được tỷ lệ trên
Số vân sáng đơn sắc cần tìm là N = N 1 + N 2 + N 3 − 2 N 12 + N 23 + N 13 = 11 + 8 + 7 − 2 2 + 0 + 3 = 16

Đáp án C
+ Trên màn, trong khoảng giữa hai vân sáng gần nhau nhất và cùng màu với vân sáng trung tâm có 8 vân sáng lục nên vân sáng lục trùng nhau là vân thứ 9: ![]()
+ Điều kiện trùng nhau của hai bức xạ: 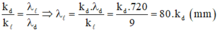
+ Theo đề bài: ![]() nên:
nên:
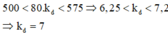
+ Giá trị của ![]()

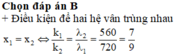
Tại M là vân sáng trùng màu với vân trung tâm, giữa M và vân trung tâm ncòn một vân sáng nữa có màu như vậy → M là vân sáng bậc 14 của bức xạ λ 1 và là vân sáng bậc 18 của bức xạ λ 2
Tại vị trí ban đầu D = 2 m, sau một phần tư chu kì màn dao động đến vị trí D' = 1 m, vì tọa độ M là không đổi, D giảm một nửa nên bậc của vân sáng tăng lên gấp đôi, vậy tại M bây giờ là vị trí vân sáng bậc 28 của λ 1 và bậc 36 của λ 2
Khi vật dịch chuyển từ vị trí ban đầu D = 2m đến vị trí D = 2 + 1 = 3 m, tương tự ta cũng xác định được tại M bây giờ là vị trí gần vân sáng bậc 10 của λ 1 và vân sáng bậc 12 của λ 2
Với thời gian 4 s là một chu kì thì số vân đơn sắc dịch chuyển qua M là : N = 2(4 + 12 + 6 + 16) = 75
Ta trừ 1 ở đây là do điểm 12 nằm ở biên nên khi màn dao động chỉ đi qua 1 lần








Chọn B