Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Chỉ cần lấy M,N thuộc hai tia đối nhau Ox và Oy sao cho OM=ON(O là chân đường cao kẻ A xuống xy) thì ta được hai đường xiên AM=AN
b:
Trường hợp 1: D trùng với H thì AD=AH
=>AD>AM
Trường hợp 2: D nằm giữa M và H
=>HD<HM
=>AD<AM(hình chiếu, đường xiên)
Trường hợp 3: D nằm giữa H và N
=>HD<HN
=>AD<AN
mà AM=AN
nên AD<AM

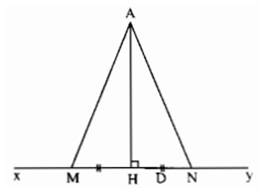
a) Phân tích bài toán: Giả sử M và N là hai điểm của đường thẳng xy mà AM = AN. Nếu gọi H là chân đường vuông góc kẻ từ điểm A đến xy thì HM, HN lần lượt là hình chiếu của các đường xiên AM, AN.
Từ AM = AN suy ra HM = HN, từ đó xác định được hai điểm M, N.
Kẻ AH vuông góc với xy (H ∈ xy)
Lấy hai điểm M, N trên xy sao cho HM = HN (1)
(dùng compa vẽ một đường tròn tâm H bán kính tùy ý; đường tròn này cắt đường thẳng xy tại hai điểm M, N thỏa mãn HM = HN)
Hai đường xiên AM, AN lần lượt có hình chiếu là HM và HN, do đó từ (1) suy ra AM = AN
b) Xét trường hợp D ở giữa M và N
- Nếu D ≡ H thì AD = AH, suy ra AD > AM (đường vuông góc ngắn hơn đường xiên)
- Nếu D ở giữa M và H thì HD < HM, do đó AD < AM (đường xiên có hình chiếu ngắn hơn thì ngắn hơn)
- Nếu D ở giữa H và N thì HD < HN, do đó AD < AN.
Theo a) ta có AM = AN nên AD < AM
Vậy khi D ở giữa M và N thì ta luôn có AD < AM
Lời giải:
a) Giả sử M và N là hai điểm của đường thẳng xy mà AM = AN.
Nếu gọi H là chân đường vuông góc kẻ từ điểm A đến xy thì HM, HN lần lượt là hình chiếu của các đường xiên AM, AN.
Từ AM = AN suy ra HM = HN, từ đó xác định được hai điểm M, N.
Kẻ AH vuông góc với xy (H ∈ xy)
Lấy hai điểm M, N trên xy sao cho HM = HN (1)
(dùng compa vẽ một đường tròn tâm H bán kính tùy ý; đường tròn này cắt đường thẳng xy tại hai điểm M, N thỏa mãn HM = HN)
Hai đường xiên AM, AN lần lượt có hình chiếu là HM và HN, do đó từ (1) suy ra AM = AN
b) Xét trường hợp D ở giữa M và N
- Nếu D ≡ H thì AD = AH, suy ra AD > AM (đường vuông góc ngắn hơn đường xiên)
- Nếu D ở giữa M và H thì HD < HM, do đó AD < AM (đường xiên có hình chiếu ngắn hơn thì ngắn hơn)
- Nếu D ở giữa H và N thì HD < HN, do đó AD < AN.
Theo a) ta có AM = AN nên AD < AM
Vậy khi D ở giữa M và N thì ta luôn có AD < AM

Nếu : ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
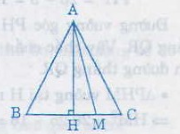
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC

Xét ΔABC có AB<AC(gt)
mà hình chiếu của AB trên BC là HB
và hình chiếu của AC trên BC là HC
nên HC>HB

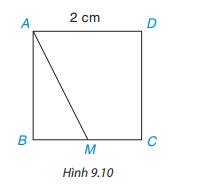
a) Đường vuông góc kẻ từ A đến BC là: AB
Đường xiên kẻ từ A đến BC là: AM
b) AB < AM (Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.)
c) Vì CB \( \bot \) AB nên khoảng cách từ C đến AB là độ dài CB = 2 cm

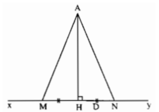
Gọi H là hình chiếu của A trên xy.
Để lấy hai điểm M, N thỏa mãn AM = AN ta vẽ 1 đường tròn tâm A, bán kính > AH cắt đường thẳng xy tại hai điểm M, N.

Sau khi vẽ theo yêu cầu đề bài, ta có:
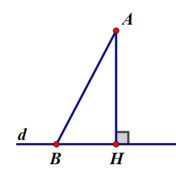
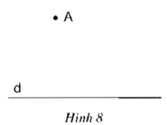
- Kẻ AH ⊥ d, H ∈ d ⇒ H là hình chiếu của A trên d
- Trên d lấy điểm B ≠ H . Nối AB ⇒ AB là đường xiên từ A đến d
Hình chiếu của đường xiên AB trên d là HB