Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3. Gọi tam giác đó là ABC với góc A vuông, các đường trung trực ứng với cạnh AB, AC lần lượt là MN,PQ; D là trung điểm cạnh huyền AC
Có : MN song song với AC và đi qua M là trung điểm của AB => N là trung điểm của BC(t/c đường trung bình) => N trùng với D
PQ song song với AB và đi qua P là trung điểm của AC => Q là trung điểm của BC(t/c đường trung bình) => Q trùng với D
MN cắt PQ tại trung điểm D của BC
Mà đường trung bình của BC đi qua D
=> Giao điểm 3 đường trung trực là D trung điểm cạnh huyền BC


a)
Ta có:
G là trọng tâm của tam giác ABC (giao điểm của ba đường trung tuyến);
H là trực tâm của tam giác ABC (giao điểm của ba đường cao);
I là giao điểm của ba đường phân giác của tam giác ABC;
O là giao điểm của ba đường trung trực của tam giác ABC (Đường trung trực đi qua trung điểm của cạnh và vuông góc với cạnh tại trung điểm đó).
Mà tam giác ABC đều nên trong tam giác ABC đường trung tuyến đồng thời là đường cao và là đường phân giác.
Vậy bốn điểm G, H, I, O trùng nhau hay nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau.
b)
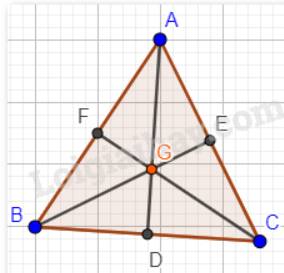
Giả sử trong tam giác ABC có hai điểm trùng nhau là H (trực tâm của tam giác) và I (giao của ba đường phân giác).
Hay AD, BE, CF vừa là đường cao, vừa là đường phân giác của tam giác ABC.
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\) ( vì AD là tia phân giác của góc BAC)
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\) (vì \(AD \bot BC\));
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta AEB = \Delta CEB\)(c.g.c). Suy ra: AB = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều hay nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.

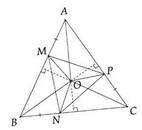
a, Vì \(\Delta ABC\) đều và \(O\) là giao điểm 3 đường trung trực nên \(AO\) là tia phân giác của \(\widehat{A}\)
\(\Rightarrow\widehat{MAO}=\dfrac{\widehat{BAC}}{2}=30^o\)
b, Tương tự a, \(\widehat{OCB}=30^o\)
Chứng minh được: \(\Delta MAO=\Delta OPC\left(c.g.c\right)\)
Ta có: \(\Delta MAO=\Delta OPC\Rightarrow OM=OP\left(1\right)\)
c, Tương tự b
\(\Delta MAO=\Delta NBO\left(c.g.c\right)\)
\(\Rightarrow ON=OM\left(2\right)\)
Từ (1) và (2) suy ra O là giao điểm
3 đương trung trực của tam giác MNP

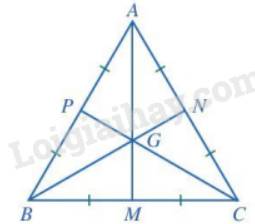
Gọi M, N, P lần lượt là các trung điểm của các đoạn thẳng BC, AC, AB.
Ta có: G là giao điểm của ba đường trung tuyến trong tam giác ABC.
Mà G cũng là giao điểm của ba đường trung trực trong tam giác ABC nên AM, BN, CP là các đường trung trực của tam giác ABC hay \(AM \bot BC;BN \bot AC;CP \bot AB\).
Xét tam giác ABM và tam giác ACM có:
AM chung;
\(\widehat {AMB} = \widehat {AMC} (= 90^\circ \))(vì \(AM \bot BC\));
BM = MC (M là trung điểm của BC).
Vậy \(\Delta ABM = \Delta ACM\)(c.g.c). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)
Tương tự ta có:
\(\Delta BNA = \Delta BNC\)(c.g.c). Suy ra: AB = BC( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều.

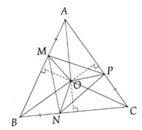
c, giao điểm 2 đường phân giác
chúc bn hok tốt!
đúng thì k cho mk nha!
mk ghi nhầm, 2 sửa thành 3 nha