Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) - Số dân tỉnh đó sau 1 năm là: \(800 + 800.r\% = 800.\left( {1 + r\% } \right)\)
- Số dân tỉnh đó sau 2 năm là: \(\begin{array}{l}800 + 800r\% + (800 + 800r\% ).r\% \\ = 800 + 1600.r\% + 800.{(r\% )^2} = 800.(1 + 2r\% + {(r\% )^2})\\ = 800{(r\% + 1)^2}\end{array}\)
- Số dân tỉnh đó sau 5 năm là: \(800.{(1 + r?\% )^5}\)
b) Ước tính số dân của tỉnh đó sau 5 năm nữa với \(r\% = 1,5\% \)là:
\(800.{(1 + 0,015)^5} = 800.(1 + {5.1^4}.0,015) = 860\) (nghìn người)

Đáp án: D
Vì 100/2 = 50 < 100 <1000/2 = 500 nên chữ số hàng trăm (số 0) không là chữ số chắc còn chữ số hàng nghìn (số 4) là chữ số chắc. 0 không là chữ số chắc thì các chữ số bên phải số 0 đều không là chữ số chắc.

Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình:
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được:
3 x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7 x + 4 y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được:
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.

TRẢ LỜI:
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.

Gọi x,y,z là số đồng tiền các loại mệnh giá 2000 đồng, 1000 đồng và 500 đồng. (\(\left(x,y,z\in N^{\circledast}\right)\).
Theo giả thiết ta có: \(x+y+z=1450\) (đồng).
Do tổng số tiền cần đổi là 1 500 000 đồng nên:
\(2000x+1000y+500z=1500000\)
Do số tiền xu loại 1 000 đồng bằng hai lần hiệu của số tiền xu loại 500 đồng với số tiền xu loại 2000 đồng nên:\(y=2\left(z-x\right)\)
Vậy ta có hệ:
\(\left\{{}\begin{matrix}x+y+z=1450\\2000x+1000y+500z=1500000\\y=2\left(z-x\right)\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=350\\y=500\\z=600\end{matrix}\right.\)
vậy số tiền loại 2000 đồng là 350 tờ; số tiền loại 1000 đồng là 500 tờ; số tiền loại 600 đồng là 600 tờ.

Chọn A.
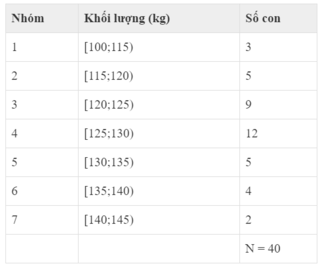
Số trung bình là:
x = 107 , 5 . 3 + 117 , 5 . 5 + 122 , 5 . 9 + 127 , 5 . 12 + 132 , 3 . 5 + 137 , 5 . 4 + 142 , 5 . 2 40 = 126

a, Sơ đồ tư duy:
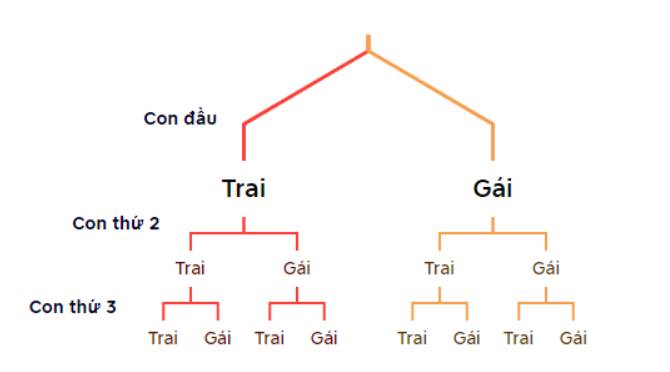
Kí hiệu con trai: T, con gái: G.
Các kết quả có thể xảy ra là: GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT.
Do đó: \(\Omega\)= {GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT}.
Vậy n(Ω) = 8.
b) Gọi biến cố A: “Gia đình đó có một con trai và hai con gái”.
Ta có: A = {GTG; TGG; GGT}. Do đó, \(n(A)\)= 3.
Vậy \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{3}{8}\)
Vì độ chính xác đến hàng trăm ( d = 150 ) nên ta quy tròn a đến hàng nghìn. Vậy số quy tròn của a là 1 718 000.
Đáp án là A.