Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xin lỗi vì đã quá trễ nhưng giải cho người khác biết =(
thì tính kgm n(Ω)= 20C3
tiếp theo mk có biến cố A : " Ba người thì trong đó ko có 1 cặp vợ chồng nào"
\(\rightarrow\overline{A}:\)" Ba người trong đó có ít nhất 1 cặp vợ chồng" ( biến cố đối)
Chọn ra 1 cặp vợ chồng từ 4 cặp : 4C1 cách
- 1 cặp đã có sẵn 2 người r mà mình đã chọn 1 cặp thì số người còn lại là 18 người
=> 18C1 cách
\(P_{\overline{A}}=\dfrac{n\overline{A}}{n\Omega}\) \(=\dfrac{4C1.18C1}{20C3}\)
=> P(A) = 1 - P(\(\overline{A}\) ) => câu D nhóa

Đáp án A
Chọn 3 tiết mục bất kỳ có: Ω = C 9 3 = 84 cách. Gọi A là biến cố: “ba tiết mục được chọn có đủ cả ba khối và đủ cả ba nội dung”. Khối 10 chọn 1 tiết mục có 3 cách, khối 11 chọn 1 tiết mục khác khối 10 có 2 cách, tương tự khối 12 có 1 cách. Ta có: Ω A = 3.2.1 = 6 cách.
Vậy P = 6 84 = 1 14 .

Đáp án A
Chọn 5 học sinh từ đội văn nghệ của nhà trường, ta xét các trường hợp
TH1. 1 học sinh lớp 12A, 2 học sinh lớp 12B và 2 học sinh lớp 12C → có C 4 1 . C 3 2 . C 2 2 = 12 cách.
TH2. 2 học sinh lớp 12A, 1 học sinh lớp 12B và 2 học sinh lớp 12C → có C 4 2 . C 3 1 . C 2 2 = 18 cách
TH3. 3 học sinh lớp 12A, 1 học sinh lớp 12B và 1 học sinh lớp 12C → có C 4 3 . C 3 1 . C 2 1 = 24 cách.
TH4. 1 học sinh lớp 12A, 3 học sinh lớp 12B và 1 học sinh lớp 12C → có C 4 1 . C 3 3 . C 2 1 = 8 cách.
TH5. 2 học sinh lớp 12A, 2 học sinh lớp 12B và 1 học sinh lớp 12C → có C 4 2 . C 3 2 . C 2 1 = 36 cách.


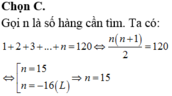
Đáp án A
Số cách xếp tiết mục đầu tiên là 1 cách.
Số cách xếp tiết mục thứ hai là 3 cách.
Số cách xếp tiết mục thứ ba là 2 cách.
Số cách xếp tiết mục thứ tư là 1 cách.
Vậy có 1.3.2.1 = 6 cách.