Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
]
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau nên hệ số góc của chúng bằng nhau g=hay y ' ( x M ) = y ' ( x N )
y = x + 1 x - 1 = 1 + 2 x - 1 ( x ≠ 1 ) ⇒ y ' = - 2 ( x - 1 ) 2
Gọi M ( x M ; 1 + 2 x M - 1 ) ; M ( x N ; 1 + 2 x N - 1 ) là hai điểm thuộc đồ thị hàm số.
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau
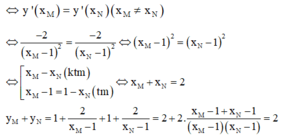
Gọi I là trung điểm của MN ta có: I (1; 1)
Dễ thấy đồ thị hàm số có TCN là y= 1và tiệm cận đứng x= 1 nên I (1; 1) là giao điểm của hai đường tiệm cận => C đúng.
TCN y= 1 và tiệm cận đứng x= 1 rõ ràng đi qua trung điểm I của đoạn MN=> B, D đúng.
Chọn A.
Từ giả thiết suy ra f(α) < g(α)
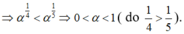
Chọn đáp án A.
Nhận xét. Ở đây ta sử dụng tính chất:
Nếu a > 1 thì a α > a β <=> α > β ;
Nếu 0 < a < 1 thì a α > a β <=> α < β .
Học sinh có thể không áp dụng tính chất trên mà giải tiếp:
Chọn D
Ta có
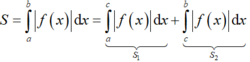
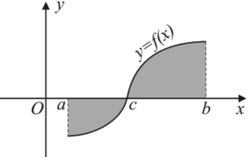
Vì f(x) < 0, ∀ x ∈ a ; c nên |f(x)| = –f(x).
Do đó, S 1 = - ∫ a c f x d x .
Tương tự, f(x) > 0, ∀ x ∈ a ; c nên |f(x)| = f(x).
Do đó, S 2 = ∫ c b f x d x .
Vậy S = - ∫ a c f x d x + ∫ c b f x d x .
Đáp án A
Gỉa sử 
Khi đó
Hơn nữa, 
Suy ra 
Tìm được M(1;-1), N(3;-3) => I(-1;1).
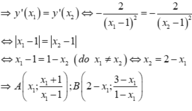
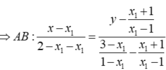
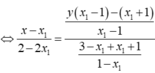
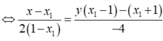
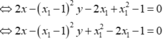
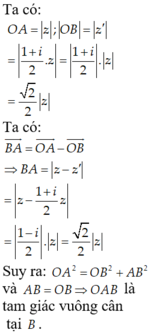
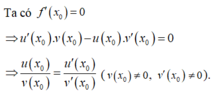
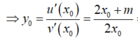
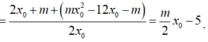
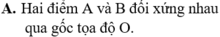
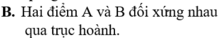
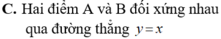
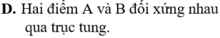
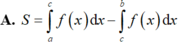
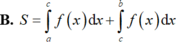
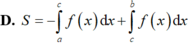
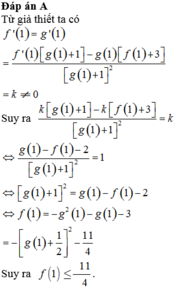
Chọn C