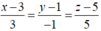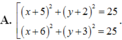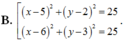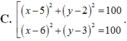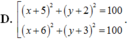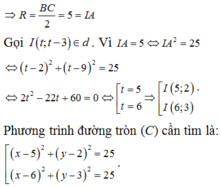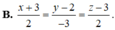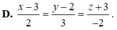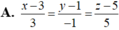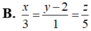Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
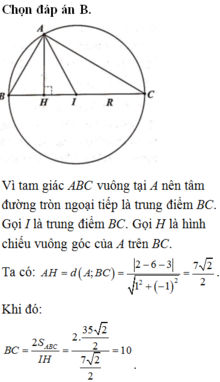
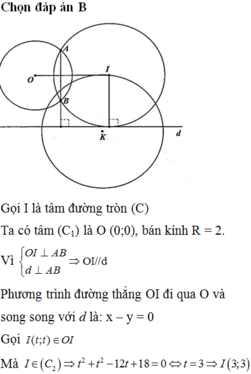
Kéo dài đường cao AH lần lượt cắt BC và đường tròn ngoại tiếp tam giác ABC tại hai điển E và K, ta dễ dàng chứng minh được E là trung điểm HK
Đường cao \(AH\perp BC\) nên có phương trình \(x-y=0\), E là giao điểm của BC và AH \(\Rightarrow E\left(4;4\right)\) và H là trung điểm \(HK\Rightarrow K\left(3;3\right)\), suy ra bán kính đường tròn ngoại tiếp tam giác ABC là \(R=IK=\sqrt{5}\)
\(\Rightarrow\) phương trình đường tròn là \(\left(x-5\right)^2+\left(y-4\right)^2=5,\left(C\right)\)
Vậy hai điểm B, C là nghiệm của hệ hai phương trình đường thẳng BC và đường tròn (C) \(\Rightarrow B\left(3;5\right);C\left(6;2\right)\) và đỉnh A là nghiệm hệ của đường cao AH và đường tròn (C) \(\Rightarrow A\left(6;6\right)\)
Diện tích tam giác ABC là :
\(S_{ABC}=\frac{1}{2}d\left(A,BC\right).BC=\frac{1}{2}\frac{\left|6+6-8\right|}{\sqrt{2}}.3\sqrt{2}=6\)
Đáp án A
=> ∆ ABC vuông tại A
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC, I(0;2;0)
Đường thẳng d qua tâm I và vuông góc mặt phẳng (ABC) được xác định
q u a I ( 0 ; 2 ; 0 ) V T C P : u → = 1 2 A B → , A C → = ( 3 ; - 1 ; 5 )
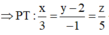
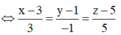
Vậy phương trình của d là x - 3 3 = y - 1 - 1 = z - 5 5
Chọn A
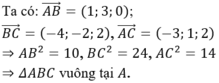
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC => I (0; 2; 0)
Đường thẳng d cần tìm đi qua I (0; 2; 0) và nhận vectơ 
làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là 
Chọn A
Ta có:
AB² = 10, BC² = 24, AC² = 14 => ∆ABC vuông tại A.
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC => I (0;2;0).
Đường thẳng d cần tìm đi qua I (0;2;0) và nhận vectơ 
làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là 