Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Công thức: Nếu I (xi ; yi) là trung điểm của AB với điểm A(xA;yA) , điểm B(xB;yB) thì:
\(x_I=\frac{x_A+x_B}{2};y_I=\frac{y_A+y_B}{2}\)
Vì I(a;b) là trung điểm của AB nên:
\(a=\frac{-3+5}{2}=1\) \(b=\frac{4+2}{2}=3\)
=> điểm I(1:3)

Ta có : Để C là trung điểm của AB thì :
\(\hept{\begin{cases}2\left(a-1\right)=1+3\\2\left(b+2\right)=2+4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=3\\b=1\end{cases}}\)

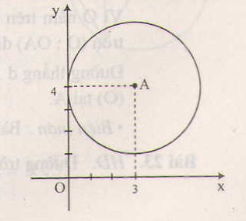
- Khoảng cách từ tâm A đến trục Ox là 4.
Vậy d>R, do đó đường tròn và trục Ox không giao nhau.
- Khoảng cách từ tâm A tới trục Oy là 3.
Vậy d=R, do đó đường tròn và trục Oy tiếp xúc nhau.

* Gọi phương trình đường thẳng AB là y = ax + b.
Tọa độ các điểm A, B phải thỏa mãn phương trình y = ax + b nên ta có:
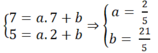
Vậy phương trình của đường thẳng AB là y = 2/5x + 21/5.
*Gọi phương trình của đường thẳng BC là y = a’x + b’.
Tương tự như trên ta có:
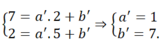
Vậy phương trình của đường thẳng BC là y = -x + 7.
*Gọi phương trình của đường thẳng AC là y = a’’x + b’’.
Tương tự như trên ta có: 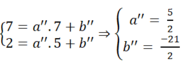
Vậy phương trình của đường thẳng AC là y = 5/2x - 21/2.