Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giao của d với trục \(Ox\) là điểm \(A\left(3;0\right)\). Phép tịnh tiến phải tìm có vectơ tịnh tiến \(\overrightarrow{v}=\overrightarrow{AO}=\left(-3;0\right)\). Đường thẳng d' song song với d đi qua gốc tọa độ nên nó có phương trình \(3x-y=0\)

Giao của d với trục Ox là điểm A(3;0). Phép tịnh tiến phải tìm có vectơ tịnh tiến v → = O A → = ( − 3 ; 0 ) . Đường thẳng d' song song với d và đi qua gốc tọa độ nên nó có phương trình 3x – y = 0.

Gọi M′ ( x′ ; y′ ) ∈ d' là ảnh của M( x , y ) ∈ d qua phép tịnh tiến theo vecto ⃗v (2;3)
\(\Rightarrow\left\{{}\begin{matrix}x'=x+2\\y'=y+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=x'-2\\y=y'-3\end{matrix}\right.\)
do M (x' ; y') \(\in\) d nên
\(3x-5y+3=0\)
\(\Rightarrow3\left(x'-2\right)-5\left(y'-3\right)+3=0\)
\(\Leftrightarrow3x'-5y'+12=0\left(d'\right)\)
vậy \(M'\left(x';y'\right)\in d':3x'-5y'+12=0\)

Gọi M′(x′;y′) ∈ d′ là ảnh của M(x,y) ∈ d qua phép tịnh tiến theo vecto v → ( 2 ; 3 )
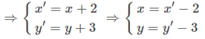
Do M(x,y) ∈ d nên
3x − 5y + 3 = 0
⇒ 3(x′−2) − 5(y′−3) + 3 = 0
⇔ 3x′ − 5y′ + 12 = 0 (d′)
Vậy M′(x′;y′) ∈ d′: 3x′ − 5y′ + 12 = 0