Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_M=2x_B-x_A=5\\y_M=2y_B-y_A=6\end{matrix}\right.\) \(\Rightarrow M\left(5;6\right)\)
Để B là trung điểm của đoạn thẳng AM, ta cần tìm tọa độ của điểm M.
Theo định nghĩa, trung điểm của một đoạn thẳng là điểm nằm ở giữa hai đầu mút của đoạn đó. Ta áp dụng công thức trung điểm để tìm tọa độ của M.
Công thức trung điểm: M(xM, yM) là trung điểm của đoạn AB <=> (xM, yM) = ((xA + xB)/2, (yA + yB)/2).
Ứng với A(1; -2) và B(3; 2): xM = (1 + 3)/2 = 2, yM = (-2 + 2)/2 = 0.
Vậy tọa độ của điểm M là M(2; 0).
Đáp án đúng là: B. M(2; 0).

Gọi tọa độ điểm \(M\) là \(M\left(x;y\right).\)
\(\overrightarrow{MA}=\left(1-x;3-y\right);\overrightarrow{MB}=\left(4-x;-y\right);\overrightarrow{MC}=\left(2-x;-5-y\right).\)
Ta có: \(\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=\overrightarrow{0}.\)
\(\left\{{}\begin{matrix}1-x+4-x-3\left(2-x\right)=0.\\3-y-y-3\left(-5-y\right)=0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-2x+5-6+3x=0.\\3-2y+15+3y=0.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=0.\\y+18=0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1.\\y=-18.\end{matrix}\right.\) \(\Rightarrow M\left(1;-18\right).\)

Tham khảo!
Gợi ý: Gọi H là trực tâm tam giác ABC. Dễ dàng chứng minh được AD là phân giác góc EDF.
=> BD là phân giác góc FDG.
=> FG đối xứng với nhau qua BC.
=> BG vuông góc GC
Vẽ đường GC tìm được tọa độ của C
Vẽ đường BC.
Gọi I là giao điểm của FG và BC tìm tọa độ của I có I rồi tìm được tọa độ của F có F thì vẽ được đường thẳng AB.

Ta thấy A,B một điểm thì thuộc trục tung, một điểm thì thuộc trục hoành nên tam giác OAB vuông tại O
=> Tâm đường tròn ngoại tiếp là trung điểm của AB
có tọa độ (2; -1)
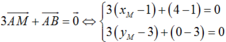
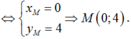
Do M thuộc Ox, gọi tọa độ \(M\left(m;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-m;-2\right)\\\overrightarrow{MB}=\left(-m;1\right)\end{matrix}\right.\)
\(MA=MB\Leftrightarrow MA^2=MB^2\)
\(\Rightarrow\left(1-m\right)^2+\left(-2\right)^2=\left(-m\right)^2+1\)
\(\Leftrightarrow m^2-2m+1+4=m^2+1\Rightarrow m=2\)
\(\Rightarrow M\left(2;0\right)\)