Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

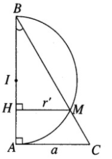
Tam giác vuông ABC có BC = 2a và AC = a nên ta suy ra ∠ ABC = 30 ° . Khi quay xung quanh trục AB cạnh BC tạo nên mặt nón tròn xoay có góc ở đỉnh bằng 60 ° và có đường tròn đáy có bán kính AC = a. Khi xoay xung quanh trục AB nửa đường tròn đường kính AB tạo nên mặt cầu có tâm là trung điểm I để đoạn AB và bán kính r = AB/2.

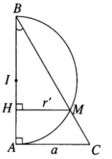
Khi quay xung quanh trục AB, giao điểm M của nửa đường tròn đường kính AB và cạnh CD sẽ tọ nên giao tuyến của mặt nón và mặt cầu.
Vẽ MH ⊥ AB
Ta có:
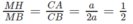
Mặt khác ta có CA 2 = CM.CB nên ta có
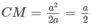
Do đó: BM = CB − CM = 3a/2 và HM = 3a/4

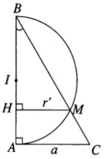
Gọi S 1 là diện tích toàn phần của hình nón và S 2 là diện tích mặt cầu.
Ta có: S 1 = πrl + πr 2 = 3 πa 2
S 2 = 4 πr 2 = 3 πa 2
Vậy S 1 = S 2


Mặt cầu (S) có tâm I(3, -2, 1) và bán kính R = 10.
Khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (α) là:
d(I, α) = ∣∣ ∣∣2.3−2.(−2)−1+9√22+(−2)2+(−1)2∣∣ ∣∣=183=6|2.3−2.(−2)−1+922+(−2)2+(−1)2|=183=6
Vì d(I, α) < R ⇒⇒ Mặt phẳng (α) cắt mặt cầu (S) theo đường tròn (C) có phương trình (C):
{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100
Tâm K của đường tròn (C) là hình chiếu vuông góc của tâm I của mặt cầu trên mặt phẳng (α).
Mặt phẳng (α) có vectơ pháp tuyến →nn→ = (2, -2. -1).
Đường thẳng d qua I và vuông góc với (α) nhận →nn→ = (2, -2, -1) làm vectơ chỉ phương và có phương trình d :
⎧⎪⎨⎪⎩x=3+2ty=−2−2tz=1−t{x=3+2ty=−2−2tz=1−t
Thay t = -2 vào phương trình của d, ta được toạ độ tâm K của đường tròn (C).
⎧⎪⎨⎪⎩x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3{x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3
⇒⇒ K(-1, 2, 3)
Ta có: IK2 = (-1 - 3)2 + (2 + 2)2 + (3 - 1)2 = 36.
Bán kính r của đường tròn (C) là:
r2 = R2 - IK2 = 102 - 36 = 64 ⇒⇒ r= 8
Giải

Mặt cầu (S) có tâm I(3, -2, 1) và bán kính R = 10.
Khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (α) là:
d(I, α) = ∣∣ ∣∣2.3−2.(−2)−1+9√22+(−2)2+(−1)2∣∣ ∣∣=183=6|2.3−2.(−2)−1+922+(−2)2+(−1)2|=183=6
Vì d(I, α) < R ⇒⇒ Mặt phẳng (α) cắt mặt cầu (S) theo đường tròn (C) có phương trình (C):
{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100{2x−2y−z+9=0(x−3)2+(y+2)2+(z−1)2=100
Tâm K của đường tròn (C) là hình chiếu vuông góc của tâm I của mặt cầu trên mặt phẳng (α).
Mặt phẳng (α) có vectơ pháp tuyến →nn→ = (2, -2. -1).
Đường thẳng d qua I và vuông góc với (α) nhận →nn→ = (2, -2, -1) làm vectơ chỉ phương và có phương trình d :
⎧⎪⎨⎪⎩x=3+2ty=−2−2tz=1−t{x=3+2ty=−2−2tz=1−t
Thay t = -2 vào phương trình của d, ta được toạ độ tâm K của đường tròn (C).
⎧⎪⎨⎪⎩x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3{x=3+2.(−2)=−1y=−2−2.(−2)=2z=1−2.(−2)=3
⇒⇒ K(-1, 2, 3)
Ta có: IK2 = (-1 - 3)2 + (2 + 2)2 + (3 - 1)2 = 36.
Bán kính r của đường tròn (C) là:
r2 = R2 - IK2 = 102 - 36 = 64 ⇒⇒ r= 8


Vậy \(S=4\pi r^2=4\pi\left(\dfrac{a\sqrt{2}}{2}\right)^2=2\pi a^2\) và \(V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi\left(\dfrac{a\sqrt{2}}{2}\right)^3=\dfrac{1}{3}\pi a^3\sqrt{2}\)








